Irradiance of light trapped between two parallel mirrors

[Sokolov]

Homework Statement

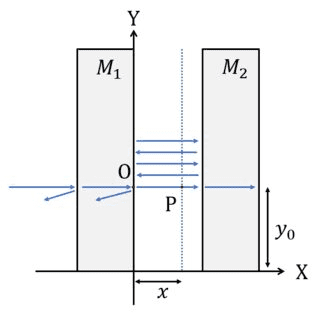
Two flat mirrors of the same reflectance $R$ are separated from each other by a distance $d$ in the air ($n=1$). A monochromatic beam of wavelength λ, linearly polarised, falls perpendicularly on the left face of $M_1$, entering the space between the two mirrors.

Let's suppose that the intensity when the beam crosses the right surface (point $O$) of the first mirror is $I_0$. Calculate the irradiance at a point $P(x,y_0)$.

Relevant Equations

Fresnel's equations

The setup of the problem is shown in the image below.

I know that I must add all the contributions of each reflected ray and that its amplitude will be reduced by a factor $r$ each time it is reflected. So after the n-th reflection, its amplitude will be $E_0r^n$, with $E_0$ the amplitude at the point $O$and $r$ the coefficient of reflection for the amplitude. However, I'm not sure about how to introduce the phase, $e^{i(ωt−kx+δ_0)}$ for each contribution.

Could anyone give me please a hint?

 

[mfb]

The attachment doesn't exist and it's hard to follow the problem statement without a sketch.

I would expect the phase to be irrelevant. The question only asks about the amplitude.

 

[Sokolov]

The attachment doesn't exist and it's hard to follow the problem statement without a sketch.

I would expect the phase to be irrelevant. The question only asks about the amplitude.

I have uploaded again the image.

The problem asks about the irradiance $I(x)$, and it is expected to have maximums and minimums depending on $x$, so I think it is relevant...

 

[mfb]

Now it works.
The phase will depend on the distance between the mirrors and the wavelength. You'll get an infinite sum that should have a nice compact formula.

 

[Dr_Nate]

The image you have is of a thing called a Fabry-Perot etalon.

In reality, to calculate the phase change you need to do a Kramers-Kronig integral of reflectivity from 0 to infinite frequency. Obviously, they didn't give you that information and the math is for experts. We usually just say that mirrors give a 180 degree phase change on reflection. I have a feeling that you won't need it though.

 

[Sokolov]

The image you have is of a thing called a Fabry-Perot etalon.

In reality, to calculate the phase change you need to do a Kramers-Kronig integral of reflectivity from 0 to infinite frequency. Obviously, they didn't give you that information and the math is for experts. We usually just say that mirrors give a 180 degree phase change on reflection. I have a feeling that you won't need it though.

I didn't write, but the problem's statement says that it is not necessary to consider rays that enter the cavity after being transmitted and reflected, this may simplify the integral.

However, how could I adjust the phase in terms of $x$ for each reflected ray?

 

[Dr_Nate]

I didn't write, but the problem's statement says that it is not necessary to consider rays that enter the cavity after being transmitted and reflected, this may simplify the integral.

However, how could I adjust the phase in terms of $x$ for each reflected ray?

I've never done the derivation myself. My suggestion is to first think of what will happen with one reflected wave. Draw it out and then write down an equation. Then do it for the second reflection. I think eventually you will see the pattern.

You might also pulling out terms from your exponential wave function that don't depend on the reflections.

 

[hutchphd]

The issue of the exact phase change on reflection will simply add a fixed additional phase shift for each reflection. It can be wavelength dependent. Just assume that the reflectance R is a complex number and proceed.

The image you have is of a thing called a Fabry-Perot etalon.

And this technique in slightly different form arises often at scattering interfaces. I have used essentially this construction to describe resonant scattering of neutral atoms from periodic surfaces. I think Fano used it to describe nuclear scattering long ago. Good stuff.

 

[Sokolov]

Ok, let's denote $E_n(x)$ the amplitude of the ray emerging from the point $n$. Then, $E_n(x)=E_0r^ne^{i(\omega t +\Lambda _n (x))}$. For the first points, the phases $\Lambda_n(x)$ will be:

$\Lambda_0(x)=-kx+\delta_0$

$\Lambda_1(x)=\Lambda_0(L)-k(L-x)+\pi=-kL+\pi+\delta_0$

$\Lambda_2(x)=\Lambda_1(L)-kx+\pi=-k(L+x)+2\pi+\delta_0$

$\Lambda_3(x)=\Lambda_2(L)-k(L-x)+\pi=-2kL+3\pi+\delta_0$

$...$

$\Lambda_n(x)=-k(nL +x )+n\pi+\delta_0$, if $n$ even

$\Lambda_n(x)=-k\Big((n-1)L\Big)+n\pi+\delta_0$ if $n$ odd

However, I find a little strange that the terms for odd $n$ doesn't have dependence on $x$... Is it possible? Or may I have done a mistake?

 

[hutchphd]

For convenience (and generality) let R (you call it r) be complex and subsume the π into it until the end. Just makes it better and easier.
What you have done is correct. But note the you will always be considering two reflections in successive terms in the sum, hence the phase will always include x as it should. Do you see?
So clean up the notation a bit and you will get a (hopefully) familiar series.

 

[Sokolov]

For convenience (and generality) let R (you call it r) be complex and subsume the π into it until the end. Just makes it better and easier.
What you have done is correct. But note the you will always be considering two reflections in successive terms in the sum, hence the phase will always include x as it should. Do you see?
So clean up the notation a bit and you will get a (hopefully) familiar series.

Ok thanks. But I don't see what you said about the two reflections... Could you explain it further?

 

[hutchphd]

Sorry I was a bit negligent and you were a little sloppy by a factor of 2 (down and back). Your original phase calculation is not quite correct the path lengths for n>0 should by 2(L-x) and 2x so that will preserve the x dependence as you noted it should. Sorry not to notice (particularly after you mentioned it!) . So the even and odd n will give right and left traveling waves.