Callmelucky
- 144
- 30
- Homework Statement
- I wonder if it's ##f(x)=2^{x}-1## considered an exponential function?
- Relevant Equations
- ##f(x)=a^{x}##
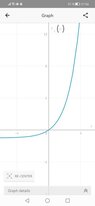
I wonder if it's ##f(x)=2^{x}-1## considered an exponential function because in my textbook it's stated that the set of values of an exponential function is a set of positive real numbers, while when graphing this function I get values(y line) that are not positive(graph in attachments), so I am not sure if the statement "the set of values of an exponential function is a set of positive real numbers" applies only to this type of function ##f(x)=a^{x}## or does it include all types of functions, like this one ##f(x)=2^{x}-1##?
Thank you
Thank you
Attachments
Last edited: