Is long division for a non-polynomic function possible?

[ecneicScience]

My question is: suppose you have a function $F(x)$ which has an asymptote at $x=x*$. Can you decompose $F(x)$ so that
$$F(x) = G(x) + H(x)$$
where $G(x)$ is defined at $x=x*$ and $H(x)$ contains the asymptotic behaviour at $x=x*$ and goes to $0$ at plus or minus $\inf$? This is commonly done when $F(x)$ is a polynomial in order to approximate $F(x)$'s behaviour with the function $G(x)$ when $x$ is sufficiently far away from $x^{*}$.

I have a very complicated function $F(x)$ that I would like to extract $G(x)$ from. If you're curious here it is:

$$F(x) = \frac{(2 a_1 z^{-a_2} -2 a_1 z^{-a_1} + z^{-a_1} - z^{-a_2}+ a_1^2 z^{-a_1} - a_2^2 z^{-a_2}) ln(z)^2 + (2 a_2 z^{-a_2} -2 a_1 z^{-a_1}+2 z^{-a_2} - 2 z^{-a_1}) ln(z) + 2 z^{-a_1} - 2 z^{-a_2}}
{(a_1 z^{-a_1} - a_2 z^{-a_2} + z^{-a_2} - z^{-a_1}) ln(z)^2 + (z^{-a_1}-z^{-a_2}) ln(z)}$$

where
$$z = 10^{x-x^{*}}$$
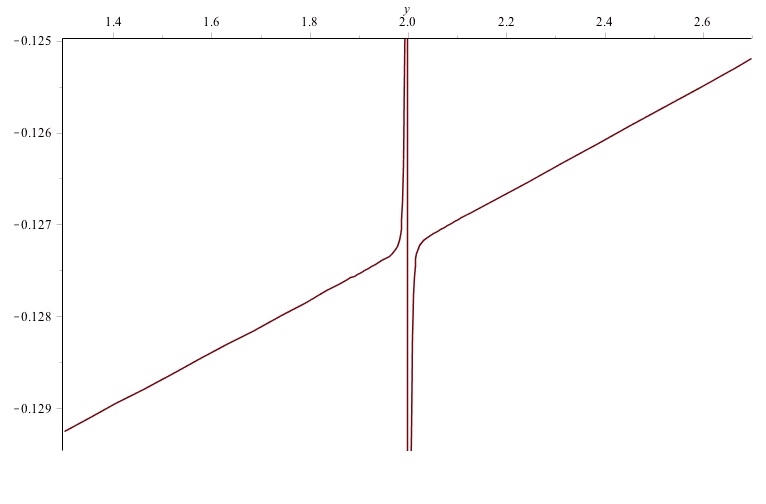
and $a_2>a_1>0$ and $x^*>0$. I've attached a graph for an instance of the function where $x^{*}=2$. As you can see there is an asymptote at $x=2$. I want either $G(x)$ or the slope of $G(x)$ at $x=x^{*}$. Has anyone encountered a similar problem?

 

[mfb]

Such a decomposition is always possible and never unique (e.g. for every solution you can add a Gaussian to G and subtract it from H). That also means that the slope of G(x) is not fixed at x=x*, it can have any value you like.

To find a possible decomposition, it is sufficient to describe the behavior either for x around x* or for x to +- infinity. The latter is probably easier here as it does not involve finding x*.

 

[ecneicScience]

Such a decomposition is always possible and never unique (e.g. for every solution you can add a Gaussian to G and subtract it from H). That also means that the slope of G(x) is not fixed at x=x*, it can have any value you like.

To find a possible decomposition, it is sufficient to describe the behavior either for x around x* or for x to +- infinity. The latter is probably easier here as it does not involve finding x*.

Thank you very much for your insight. You made the arbitrariness of G(x) very clear to me. Sorry it took so long to get back to you.