Nirmal Padwal
- 41
- 2
- Homework Statement
- The ##W^−## was discovered in 1983 at CERN using proton-antiproton scattering
$$p + \bar{p} \to W^- + X$$,
where ##X## represents one or more particles. What is the most likely ##X## for this process?
Draw a Feynman diagram for your reaction, and explain why your ##X## is more probable than the various alternatives?
- Relevant Equations
- (Not applicable)
I think ##X## appears to be ##\pi^{+}## because it is light and energetically more favourable. Pion should be positive to ensure charge conservation. I am stuck at drawing a Feynman diagram for $$p+\bar{p} \to W^- + \pi^+$$.
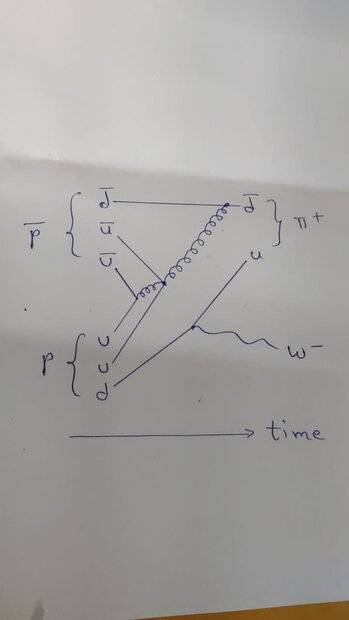
Is this correct? Is this the leading order diagram or is there a diagram with fewer vertices possible? I tried seeing if a digram with fewer vertices is possible but this is the best I am able to do.
Is this correct? Is this the leading order diagram or is there a diagram with fewer vertices possible? I tried seeing if a digram with fewer vertices is possible but this is the best I am able to do.