Is the Molar Specific Heat of Air Similar to Hydrogen?

[Karfen]

Homework Statement

Estimate the molar specific heat of the air at constant volume Cv by taking into account
major molecules in the air. Plot it as a function of absolute temperature and discuss its
significance.

Relevant Equations

The major chemical elements of air are nitrogen(78%) and oxygen(22%).

The molar specific heat of the air at constant volume for diatomic molecule:
Cv=3/2R (Low Temperature)
Cv=5/2R(High Temperature)
Cv=7/2R(Higher Temperature)

And this is the Cv graph for hydrogen:

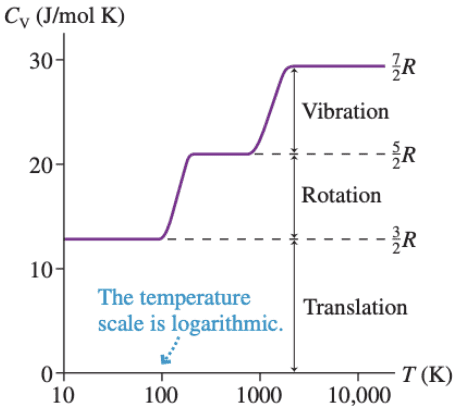
I think the Cv graph for air is similar with this graph. But I don't know the answer, can someone tell me?

 

[mfb]

Oxygen and nitrogen are somewhat similar to hydrogen for the purpose of this question.

What is room temperature in Kelvin, very roughly? Where in this graph are we?

 

[haruspex]

Oxygen and nitrogen are somewhat similar to hydrogen for the purpose of this question.

Is that true? At https://en.wikipedia.org/wiki/Molar_heat_capacity I read:
"For the rotational degrees of freedom, the thawing temperature is usually a few tens of kelvins (although with a very light molecule such as hydrogen the rotational energy levels will be spaced so widely that rotational heat capacity may not completely "unfreeze" until considerably higher temperatures are reached)."