Discussion Overview
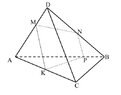
The discussion revolves around the geometric feasibility of a plane MKPN existing within a pyramid ABCD, specifically addressing whether points M, K, P, and N can lie on the pyramid's sides while forming a valid plane. The scope includes geometric axioms and properties related to tetrahedrons and pyramids.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- Some participants assert that it is possible to slice a tetrahedron with a plane, suggesting that such a configuration can exist.
- Others clarify the distinction between a pyramid and a tetrahedron, noting that a tetrahedron has four triangular faces and no rectangular face, while a pyramid has a polygonal base.
- A participant points out that while any three points can define a plane, the specific points M, K, P, and N may not all lie on a single plane depending on their placement on the edges.
- One participant proposes a proof involving three-dimensional analytic geometry to show that a plane defined by points on the edges intersects another edge at a point within the tetrahedron.
- Another participant expresses concern that the configuration may violate the axiom that two planes intersect in a straight line, questioning the validity of the proposed plane MKPN.
- Some participants argue that if points M, N, and P lie on the same face of the tetrahedron, then point K cannot lie in the same plane, rendering the configuration impossible.
- There is acknowledgment of confusion regarding the placement of points and the implications for the existence of the plane.
Areas of Agreement / Disagreement
Participants express differing views on the possibility of the plane MKPN existing within the pyramid ABCD. While some argue for its feasibility, others contend that the configuration is impossible due to geometric constraints. The discussion remains unresolved regarding the validity of the proposed plane.
Contextual Notes
Participants note that the discussion involves complex geometric properties and may depend on the specific definitions and placements of points within the pyramid. The proof mentioned requires advanced understanding of three-dimensional geometry.