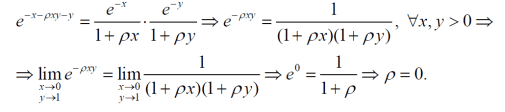SUMMARY
The discussion centers on the proof of the condition that ρ must equal zero for the identity exp(-ρxy) = 1/((1+ρx)(1+ρy)) to hold for all x, y > 0. Participants debate whether the proof is universal or limited to specific limits, emphasizing the importance of continuity and the implications of finding particular values of x and y. It is concluded that while ρ = 0 is a solution, the challenge lies in demonstrating that it is the only solution applicable across all x and y values.
PREREQUISITES
- Understanding of mathematical identities and proofs
- Familiarity with limits and continuity in calculus
- Knowledge of exponential functions and their properties
- Basic algebraic manipulation skills
NEXT STEPS
- Study the concept of mathematical identities and their proofs
- Learn about limits and continuity in calculus
- Explore the properties of exponential functions in depth
- Practice algebraic manipulation with complex equations
USEFUL FOR
Mathematicians, students studying calculus or algebra, and anyone interested in understanding the nuances of mathematical proofs and identities.