- #1
ezadam
- 21
- 0
Hey guys,
I am having some problems with the concept of inertial/non-inertial frames of reference and their applications in engineering dynamics. So I've learned that a given frame of reference is defined to be non-inertial when something in the studied system can only be explained through fictitious forces such as the Centrifugal one.
Now, let's take as an example the motion of a block that can slide freely on a frictionless arm that rotates in a horizontal planewith a constant rate over a hinge. Here's a sketch of what I'm talking about:
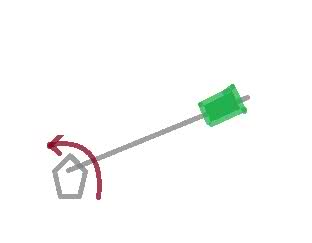
So if we look into the radial direction of the block's motion, we find that there is no force acting in such a direction and thus accordingly, the block should theoretically not move in the radial direction. Surprisingly, that is not what happens as the block slides away due to its inertia.
Now how come does that happen if there are no radial forces ? Does that mean (according to my initial definition) that I should have accounted for some centrifugal force and thus that my somewhat rough force analysis should be based on a non-inertial frame of reference, ergo that radial/transverse force analysis is not an inertial reference frame ? Or do I have some huge misconception about the issue ?
Thanks in advance
I am having some problems with the concept of inertial/non-inertial frames of reference and their applications in engineering dynamics. So I've learned that a given frame of reference is defined to be non-inertial when something in the studied system can only be explained through fictitious forces such as the Centrifugal one.
Now, let's take as an example the motion of a block that can slide freely on a frictionless arm that rotates in a horizontal planewith a constant rate over a hinge. Here's a sketch of what I'm talking about:
So if we look into the radial direction of the block's motion, we find that there is no force acting in such a direction and thus accordingly, the block should theoretically not move in the radial direction. Surprisingly, that is not what happens as the block slides away due to its inertia.
Now how come does that happen if there are no radial forces ? Does that mean (according to my initial definition) that I should have accounted for some centrifugal force and thus that my somewhat rough force analysis should be based on a non-inertial frame of reference, ergo that radial/transverse force analysis is not an inertial reference frame ? Or do I have some huge misconception about the issue ?
Thanks in advance
 , you're going to have to convince yourself on this one …
, you're going to have to convince yourself on this one …