High School Is the time derivate of force equal to the position derivative power?

Click For Summary
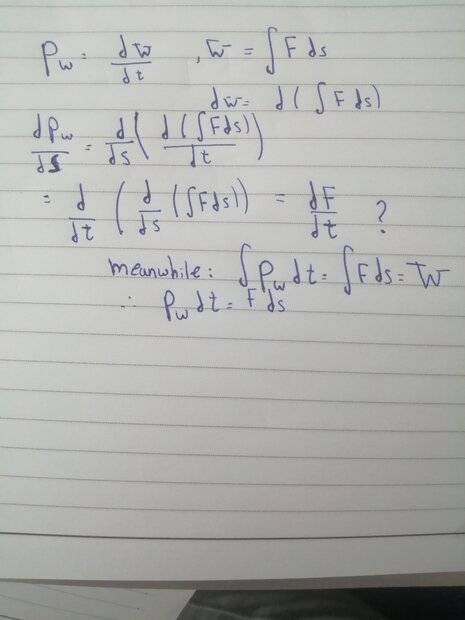
The discussion centers on whether the time derivative of force is equivalent to the position derivative of power. It is noted that this concept may seem nonsensical at first glance. However, it is clarified that for a varying force applied at constant speed, the two derivatives can indeed be related. The conversation highlights the importance of understanding the context of force and power in physics. Overall, the relationship between these derivatives is complex and requires careful consideration.
highschoolstudent454
Messages
5
Reaction score
0
Is this wrong?
IMG_20240508_194157.jpg
 
Physics news on Phys.org
It is quite nonsensical.
 
highschoolstudent454 said:
Is the time derivate of force equal to the position derivative power?
For a varying force applied at constant speed, yes.
 

Thread 'Mousetrap Car Energy efficiency'

For simple comparison, I think the same thought process can be followed as a block slides down a hill, - for block down hill, simple starting PE of mgh to final max KE 0.5mv^2 - comparing PE1 to max KE2 would result in finding the work friction did through the process. efficiency is just 100*KE2/PE1. If a mousetrap car travels along a flat surface, a starting PE of 0.5 k th^2 can be measured and maximum velocity of the car can also be measured. If energy efficiency is defined by...
View full post »

Similar threads

Undergrad Deriving kinematic equation for position
  • · Replies 53 ·
2
Replies
53
Views
4K
High School Deriving v(t) from F(x), for Linear Motion
  • · Replies 1 ·
Replies
1
Views
1K
High School How hydraulic pressure can change the magnitude of a force?
  • · Replies 7 ·
Replies
7
Views
655
Who Exerts Gravity Power? Force x Velocity Dot Product
  • · Replies 19 ·
Replies
19
Views
2K
Undergrad My textbook is deriving wave speed on a string under tension
  • · Replies 19 ·
Replies
19
Views
2K
Relationship between force and potential energy
  • · Replies 35 ·
2
Replies
35
Views
6K
Undergrad Sound pressure and inverse distance law
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Dynamics of systems of material points
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Time derivative using the quotient rule
  • · Replies 1 ·
Replies
1
Views
871
Undergrad 3D Printed Piston | Lower mass = Power
  • · Replies 41 ·
2
Replies
41
Views
4K