Is the Variational Principle an introductory example for Calculus of Variations?

[mathmari]

Hey!

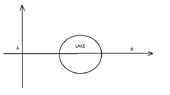
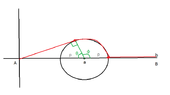
We want to get from the poit $A$ to the point $B$ avoiding the lake. How should we move to minimize the distance?

View attachment 4795

There are the following possibilities:
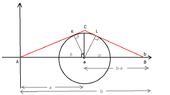
1.
View attachment 4794

(We go along the red lines)

In this case the distance is the following:

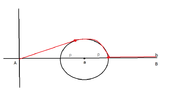
Let $y_1$ be the first red line and $y_2$ the second one. Then from the Pythagorean theorem we have the following:
$$y_1^2=a^2+p^2 \Rightarrow y_1=\sqrt{a^2+p^2} \\ y_2^2=(b-a)^2+p^2 \Rightarrow y_2=\sqrt{(b-a)^2+p^2}$$

So the length of the way is equal to $y_1+y_2$. Is this correct? 2.
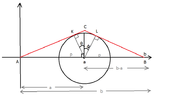
View attachment 4796

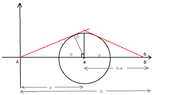
To find the the lengh ofthe first red line we apply the pythagorean theorem, right? So let $x$ be this part, then $a^2=x^2+p^2 \Rightarrow x=\sqrt{a^2-p^2}$. The last part of the red line is equal to $b-a$. How can we find the length of the red part of the circle? 3.
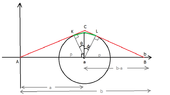
View attachment 4797

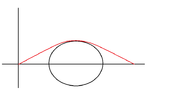
How can we find in this case the length of the red line?

 

[I like Serena]

1.
In this case the distance is the following:
Let $y_1$ be the first red line and $y_2$ the second one. Then from the Pythagorean theorem we have the following:
$$y_1^2=a^2+p^2 \Rightarrow y_1=\sqrt{a^2+p^2} \\ y_2^2=(b-a)^2+p^2 \Rightarrow y_2=\sqrt{(b-a)^2+p^2}$$

So the length of the way is equal to $y_1+y_2$. Is this correct?

Hi mathmari! (Smile)

I don't think so...

Isn't the distance $y_1$ to the top of the lake instead of slightly higher as it should be? (Wondering)

2.
To find the the lengh ofthe first red line we apply the pythagorean theorem, right? So let $x$ be this part, then $a^2=x^2+p^2 \Rightarrow x=\sqrt{a^2-p^2}$. The last part of the red line is equal to $b-a$. How can we find the length of the red part of the circle?

The length along a circle with radius $p$ is $p\Delta\phi$ where $\phi$ is the angle that is traversed. (Nerd)

3.
How can we find in this case the length of the red line?

It's a combination of (1) and (2).
First we travel in a straight line to the point that touches the lake.
Then we travel along the circumference of the lake.
After which we continue in a straight line to the destination. (Thinking)

 

[mathmari]

I don't think so...

Isn't the distance $y_1$ to the top of the lake instead of slightly higher as it should be? (Wondering)

What do you mean? (Thinking)

The length along a circle with radius $p$ is $p\Delta\phi$ where $\phi$ is the angle that is traversed. (Nerd)

Is it as follows?

View attachment 4798

$$\cos \theta=\frac{p}{a} \Rightarrow \cos (\pi -\phi )=\frac{p}{a} \Rightarrow \cos (\phi )=-\frac{p}{a} \Rightarrow \phi =\arccos \left (-\frac{p}{a}\right )$$

It's a combination of (1) and (2).
First we travel in a straight line to the point that touches the lake.
Then we travel along the circumference of the lake.
After which we continue in a straight line to the destination. (Thinking)

Is it as follows?

$$\sqrt{a^2-p^2}+p\Delta \phi +\sqrt{(b-a)^2-p^2}$$

 

[I like Serena]

What do you mean? (Thinking)

Which are the sides of the Pythagorean triangle exactly?
Does the hypotenuse correspond to the full length of the red line? (Wondering)

Is it as follows?

$$\cos \theta=\frac{p}{a} \Rightarrow \cos (\pi -\phi )=\frac{p}{a} \Rightarrow \cos (\phi )=-\frac{p}{a} \Rightarrow \phi =\arccos \left (-\frac{p}{a}\right )$$

Yup. (Nod)

Is it as follows?

$$\sqrt{a^2-p^2}+p\Delta \phi +\sqrt{(b-a)^2-p^2}$$

Yep. (Smile)

 

[mathmari]

Which are the sides of the Pythagorean triangle exactly?
Does the hypotenuse correspond to the full length of the red line? (Wondering)

View attachment 4801

$$(AK)=\sqrt{a^2-p^2} \ \ , \ \ (LB)=\sqrt{(b-a)^2-p^2}$$

Can we find the length of the parts $KC$ and $CL$ ?

 

[I like Serena]

$$(AK)=\sqrt{a^2-p^2} \ \ , \ \ (LB)=\sqrt{(b-a)^2-p^2}$$

Can we find the length of the parts $KC$ and $CL$ ?

Sure!
$$\tan\theta=\frac P{KC}$$

 

[mathmari]

Sure!
$$\tan\theta=\frac P{KC}$$

Is it as follows?

View attachment 4802

$$\cos \theta =\frac{p}{a} \Rightarrow \theta=\arccos \left (\frac{p}{a}\right ) \\ \tan \theta=\frac{(KC)}{p} \Rightarrow (KC)=p \tan \theta , \text{ with } \theta=\arccos \left (\frac{p}{a}\right )$$

and

$$\cos \phi =\frac{p}{b-a} \Rightarrow \phi=\arccos \left (\frac{p}{b-a}\right ) \\ \tan \phi=\frac{(CL)}{p} \Rightarrow (CL)=p \tan \phi , \text{ with } \phi=\arccos \left (\frac{p}{b-a}\right )$$

 

[mathmari]

Are the total lengths at each case the following?

1. $$\sqrt{a^2-p^2}+p\tan \theta+p\tan \phi +\sqrt{(b-a)^2-p^2}$$
   
2. $$\sqrt{a^2-p^2}+p\arccos \left (-\frac{p}{a}\right )+b-a-p$$
   
3. $$\sqrt{a^2-p^2}+p\left (\pi -\arccos \left (\frac{p}{a}\right )-\arccos \left (\frac{p}{b-a}\right )\right )+\sqrt{(b-a)^2-p^2}$$

Having this information, how do we know which of them is the minimum?

 

[I like Serena]

Is it as follows?



$$\cos \theta =\frac{p}{a} \Rightarrow \theta=\arccos \left (\frac{p}{a}\right ) \\ \tan \theta=\frac{(KC)}{p} \Rightarrow (KC)=p \tan \theta , \text{ with } \theta=\arccos \left (\frac{p}{a}\right )$$

and

$$\cos \phi =\frac{p}{b-a} \Rightarrow \phi=\arccos \left (\frac{p}{b-a}\right ) \\ \tan \phi=\frac{(CL)}{p} \Rightarrow (CL)=p \tan \phi , \text{ with } \phi=\arccos \left (\frac{p}{b-a}\right )$$

With the angle for $\theta$ that you picked, I think it should be: $\sin \theta =\frac{p}{a}$.

Are the total lengths at each case the following?

1. $$\sqrt{a^2-p^2}+p\tan \theta+p\tan \phi +\sqrt{(b-a)^2-p^2}$$
   
2. $$\sqrt{a^2-p^2}+p\arccos \left (-\frac{p}{a}\right )+b-a-p$$
   
3. $$\sqrt{a^2-p^2}+p\left (\pi -\arccos \left (\frac{p}{a}\right )-\arccos \left (\frac{p}{b-a}\right )\right )+\sqrt{(b-a)^2-p^2}$$

Having this information, how do we know which of them is the minimum?

That looks correct.

Well, in (1) we can shorten the length by pulling the intersection at the top down to the lake.
In (2) we can shorten the length by pulling the angle on the right hand side of the lake outward.

It's only in (3) that there is nothing that we can do to shorten the length.
Moreover, wherever we pull a bit on the path, in the "first order" the length won't even change.
This confirms that according to the Variational Principle, it's an optimal path.

 

[mathmari]

With the angle for $\theta$ that you picked, I think it should be: $\sin \theta =\frac{p}{a}$.

Why is it $\sin$ and not $\cos$ ?

Well, in (1) we can shorten the length by pulling the intersection at the top down to the lake.

Do you mean that we can shorten the length by the following green line?

View attachment 4808

In (2) we can shorten the length by pulling the angle on the right hand side of the lake outward.

What exactly do you mean?

It's only in (3) that there is nothing that we can do to shorten the length.
Moreover, wherever we pull a bit on the path, in the "first order" the length won't even change.
This confirms that according to the Variational Principle, it's an optimal path.

What exactly is the Variantonal Principle?

 

[I like Serena]

Why is it $\sin$ and not $\cos$ ?

Because the angle $\theta$ that you picked, is the same as the angle at $A$.
And the sine of the angle at $A$ is $\frac p a$.

Do you mean that we can shorten the length by the following green line?

Yes.

What exactly do you mean?

We can shorten the path by making it more like (3), removing the angle at the right hand side of the lake.

What exactly is the Variantonal Principle?

The Variational Principle lies at the root of Calculus of Variations.

In essence it says that if some path solution doesn't become better in the first order if you change it anywhere, it's an optimal solution.

We can compare it to thinking of an elastic string.
If we put an elastic string on the red path and tighten it, both solutions (1) and (2) will change until they reach solution (3), which is the tightest possible.

Since you have already asked a question about Calculus of Variations in the chat room, can it be that this is an introductory example? (Wondering)