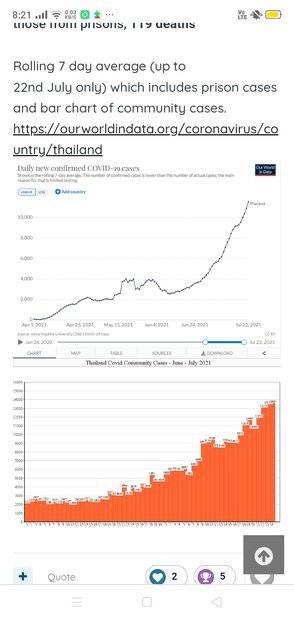
SUMMARY
The discussion centers on the classification of a curve derived from an orange bar graph, questioning whether it is quadratic or exponential. The user references the differential equation dy/dt = ky, indicating an exponential growth model typical in infectious disease dynamics. They highlight the impact of external factors, such as lockdowns and vaccination efforts, which may distort the expected exponential behavior, potentially leading to a quadratic appearance in the data. Relevant resources include online calculators for SIR models and a research paper that further explores these modeling issues.
PREREQUISITES
- Understanding of differential equations, specifically dy/dt = ky
- Familiarity with SIR models in epidemiology
- Knowledge of data interpretation in the context of infectious diseases
- Basic statistical analysis to assess curve fitting
NEXT STEPS
- Research SIR model calculations using online tools
- Study the paper on quadratic versus exponential modeling in infectious disease
- Explore the implications of lockdowns on exponential growth patterns
- Learn about curve fitting techniques in statistical analysis
USEFUL FOR
Mathematicians, epidemiologists, public health officials, and data analysts interested in modeling infectious disease spread and understanding the implications of external factors on growth curves.