- #1
- 25,839
- 258
(the story so far … I maintain that, inside an event horizon, there is a useful distinction between "space" and "space-like" dimensions, and that in any realistic coordinate system, time is space-like. JesseM maintains that, in any realistic coordinate system, time must be time-like.
JesseM maintains that, "in a local coordinate system constructed out of freefalling rulers and clocks, the laws of physics must look identical to those of SR." I maintain that this is not possible … that inside an event horizon, the laws of physics are the same, but the geometry is different, and therefore the physics must look different.
now read on … )
)
 conservation of mass
conservation of mass  Hi JesseM!
Hi JesseM! 
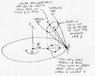
a thought experiment …
In Schwarzschild coordinates, imagine a free-falling observer inside an event horizon. His path is the axis of two "cylinders" of free-falling particles, following him, but faster.
He can see them until they hit his backward light-cone ("diagonal" light does go fast enough for that). And the light by which he seems them reaches him at the same time from both "cylinders".
In your SR-physics local coordinate system, what happens to these "cylinders" when they hit the Schwarzschild light-cone?
Doesn't the Schwarzschild light-cone become a coordinate singularity which swallows them up? And isn't that singularity on the same radius as the observer?
So each "cylinder" converges to an event (possibly "at infinity") whose displacement from him is light-like … and either it is ahead of him, so he sees the particles disappearing in his own future … or it is behind him, in which case he literally has a singularity in his wake, and where is there room for the rest of space-time to fit in?
Or is it in his own present (as the Schwarzschild system requires)?
(And we can shrink the inside "cylinder", so that that event can be as "close" to the observer as we like.)
And, if the laws of physics are the same as in SR, doesn't this coordinate singularity have to be an actual singularity … which it obviously isn't?
And, if the laws of physics are the same as in SR (and if he can't see infinitely far into the future):
 what happened to the mass?
what happened to the mass? 
JesseM maintains that, "in a local coordinate system constructed out of freefalling rulers and clocks, the laws of physics must look identical to those of SR." I maintain that this is not possible … that inside an event horizon, the laws of physics are the same, but the geometry is different, and therefore the physics must look different.
now read on …
a thought experiment …
In Schwarzschild coordinates, imagine a free-falling observer inside an event horizon. His path is the axis of two "cylinders" of free-falling particles, following him, but faster.
He can see them until they hit his backward light-cone ("diagonal" light does go fast enough for that). And the light by which he seems them reaches him at the same time from both "cylinders".
In your SR-physics local coordinate system, what happens to these "cylinders" when they hit the Schwarzschild light-cone?
Doesn't the Schwarzschild light-cone become a coordinate singularity which swallows them up? And isn't that singularity on the same radius as the observer?
So each "cylinder" converges to an event (possibly "at infinity") whose displacement from him is light-like … and either it is ahead of him, so he sees the particles disappearing in his own future … or it is behind him, in which case he literally has a singularity in his wake, and where is there room for the rest of space-time to fit in?
Or is it in his own present (as the Schwarzschild system requires)?
(And we can shrink the inside "cylinder", so that that event can be as "close" to the observer as we like.)
And, if the laws of physics are the same as in SR, doesn't this coordinate singularity have to be an actual singularity … which it obviously isn't?
And, if the laws of physics are the same as in SR (and if he can't see infinitely far into the future):