Discussion Overview
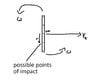
The discussion revolves around understanding the kinetic energy available during off-center impacts of rotating and translating rigid bodies, particularly in the context of ancient thrown weaponry. Participants explore the principles governing energy transfer during such impacts, considering both linear and rotational kinetic energy in the scenario of inelastic collisions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- One participant seeks to understand how to quantify the kinetic energy available in an off-center impact, noting that the energy transferred may vary depending on the side of impact relative to the direction of motion.
- Another participant mentions that in completely inelastic collisions, linear kinetic energy is not conserved, and the remaining rotational kinetic energy can be determined from conserved angular momentum.
- A participant acknowledges the distinction between elastic and inelastic collisions, emphasizing a focus on the kinetic energy available in the impact rather than the specifics of the collision type.
- One participant critiques the oversimplification of the collision scenario, suggesting that the dynamics of the impact should consider the relative motion of the bodies involved.
- Another participant notes that the change in momentum from the impact would need to be analyzed in terms of both linear and angular components to determine the resulting energies.
- A participant expresses uncertainty about having encountered a straightforward solution, indicating a lack of formal training in physics.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and approaches to the problem, with no consensus reached on a definitive method for calculating the kinetic energy in off-center impacts. Multiple competing views on the treatment of energy and momentum in inelastic collisions are present.
Contextual Notes
Limitations include potential oversimplifications in modeling the collision dynamics and the dependence on specific definitions of energy transfer in the context of rigid body impacts.