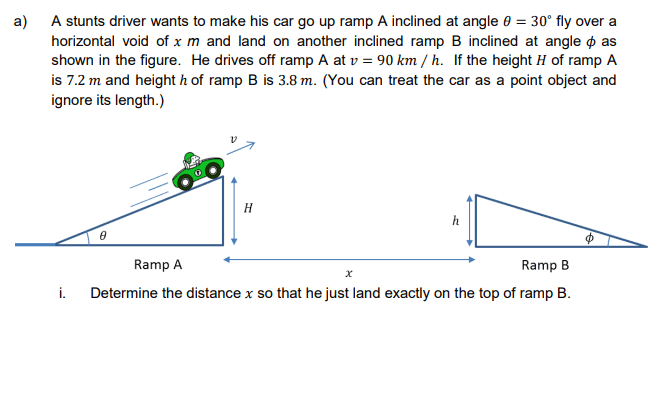
nicky670 said:
okay so i wanted to find the time taken for the car to travel from start point to end point. And if i substitute the into the equation, will be 7.2 = 25sin30t - 0.5(9.8)t^2. But the t that i got is wrong from the answer, and so if i want to find the x distance when i substitute the t inside, i will get the wrong answer. What am i doing wrong?
Your error is in the application of that equation.

You will realize it as you respond the question in post #8 above.
“The time taken for the car to travel from start point to end point” horizontally is the same time taken for the car to vertically move up and down.
As the problem allows you to disregard the frictional drag of the air, we could say that the car will rise and fall only under the influence of the constant acceleration of gravity g all the time.
Assuming the same absence of air resistance, you could throw a ball or stone straight upwards at the same ##V_{iy}=12.5~m/s## that you have calculated and it would reach the same height relative to your hand that the car reaches respect to the departure point of ramp A.
You can easily calculate the time taken by the ball (or the car) to reach the peak or its highest point, let’s call it ##t_{up}##.
That ball would take the same amount of seconds in its way down than it took in its way up and it would land in your hand with a downwards velocity of 12.5 m/s.
If instead, the ball misses your hand and lands on a surface located several meters lower than your hand, the taken time to fall from the peak to that surface, as well as the landing velocity would be greater than the at-the-hand values.
Since the vertical up and down heights of the ball (as well as of your car) are not symmetrical, we could say that:
##Total~flight~time~=~t_{up}+t_{down}##
Applying that total flight time to the horizontal movement of the car, you could calculate the x distance between take-off and landing points of your car.