Knowing when to decompose weight vector vs. normal vector

[TRB8985]

Homework Statement

Knowing whether there is a "correct" way to approach breaking down vectors by decomposing the normal force compared to the weight.

Relevant Equations

F = ma ; W = mg

Good afternoon everyone,

I have a question on Newton's 2nd Law regarding objects on a generic incline. Take for example, a car on a banked curve:

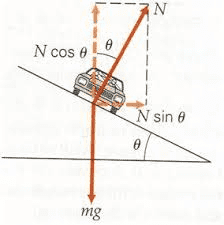Here in the picture I've provided, you can see that the normal force has been decomposed into the x and y components via sine and cosine of the angle multiplied by N.

My question is.. is there a particular reason that seems to be the norm? When I was an undergraduate, I seemed to always be under the impression that the normal was strictly perpendicular to a surface, and instead, it was the weight vector that was decomposed with the coordinate system parallel to the tilted surface, like this:

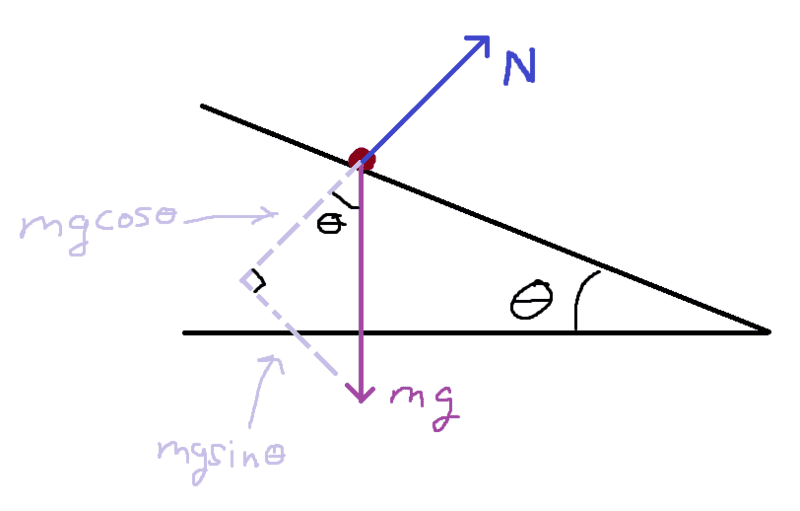My initial thought was that these were equivalent ways of approaching the same idea. Just wanted to be sure.

 

[kuruman]

First of all, the acceleration of the system will be the same regardless how you draw your $x$ and $y$ axes in terms of which you write your vectors. Nature doesn't know the alphabet. The rule of thumb is that if you have two-dimensional situations, as in the one above, you choose axes so that the acceleration is along one of the principal axes.

This is recommended but not cast in stone. It makes Newton's second law equations easier to handle because the acceleration is zero in the other direction. In the example of the car going around the curve, the acceleration is horizontal so the $x$-axis is along the horizontal. In the example of the block sliding down, the acceleration is along the incline, so it makes sense to choose the $x$-axis down the incline.

As an exercise, you might wish to (try and) solve either problem using different axes and see how much more involved it gets mathematically. Nevertheless, if you do everything right, the answer will be the same.

 

[TRB8985]

Great, glad to hear it.

That actually sounds like a good idea for a YouTube video.. Thanks, Kuruman!

 

[kuruman]

Good luck.

 

[Delta2]

In the example of the car going around the curve, the acceleration is horizontal so the x-axis is along the horizontal

The centripetal (normal) acceleration is along the x-axis, the car might as well have tangential acceleration along the z-axis (perpendicular to the plane of the page). But yes in general we choose the axis so that the acceleration (normal or tangential) is along one of the axis.

 

[haruspex]

The centripetal (normal) acceleration

Just to clarify, "normal" there is in relation to the velocity vector, not in relation to the plane.

 

[Delta2]

Just to clarify, "normal" there is in relation to the velocity vector, not in relation to the plane.

Yes I mean normal to the velocity vector $\mathbf{v}$ or normal to the trajectory infinitesimal element $d\mathbf{l}=\mathbf{v}dt$.