karush
Gold Member
MHB
- 3,240
- 5
nmh{1000} ov 346.21
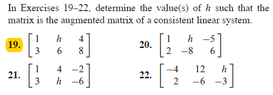
ok I am trying to these 4 problems
but don't think I understand the augmented process
these are the answers to 19 and 21

$\tiny{1.1.19}$
$$A_{19}=\left[\begin{array}{rrrrr}
1& \,h& \,4\\
3& \, 6& \, 8
\end{array}\right]$$$\textit{so if we multiply $R_1$ by subtract from R_3 we have}$\\
$$\left[\begin{array}{rrrrr}
1& \,h& \,4\\
0& \, (6-3h)& \, -4
\end{array}\right]$$uhmmm ?
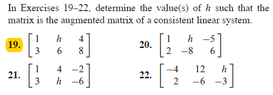
ok I am trying to these 4 problems
but don't think I understand the augmented process
these are the answers to 19 and 21
$\tiny{1.1.19}$
$$A_{19}=\left[\begin{array}{rrrrr}
1& \,h& \,4\\
3& \, 6& \, 8
\end{array}\right]$$$\textit{so if we multiply $R_1$ by subtract from R_3 we have}$\\
$$\left[\begin{array}{rrrrr}
1& \,h& \,4\\
0& \, (6-3h)& \, -4
\end{array}\right]$$uhmmm ?
Last edited: