Ladder resting against wall(equilibrium)

[dvvv]

Homework Statement

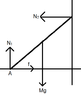
A uniform ladder rests against a smooth wall and a rough floor with a coefficient of friction 1/2. Find the angle at which the ladder slips.

Homework Equations

N = mg?
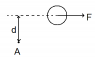
M = d*F

The Attempt at a Solution

I said N1 was the normal force from the floor onto the ladder, and [STRIKE]N1[/STRIKE] N2 was the normal force from the wall onto the ladder. The frictional force is 1/2*N1.
I put the vertical and horizontal forces equal to each other and I got
N1 = mg
and N2 = 1/2*N1 = 1/2*mg

Then I should put the anti-clockwise and clockwise moments equal to each other, although I'm not really sure how to do this part.

 

[SammyS]

Use a free body diagram for the ladder.

I assume you meant to say that N₂ is the normal force the wall exerts on the ladder.

Find the moments about some point on the ladder, I suggest using the point at which the ladder contacts the ground.

Assuming that the ladder has uniform mass distribution, its center of mass is at its center.

It's as if the force of gravity acts at the ladder's center of mass.

 

[cupid.callin]

if you take net torque to be equal to 0 at A

so torque due to mg = torque due to N2

n1 and f has 0 torques

 

[SammyS]

@ cupid.callin.

I see that our responses were ~2 minutes apart. They compliment each other quite well.

Looking at this problem reminds me of that ladder problem in that list of questions you posted a while back. Usually the wall doesn't produce much friction, so I think the ladder's bottom is more likely to "kick out" when a person is near the top, rather than near the bottom. (The person on the ladder may be viewed as shifting the C.M. up or down the ladder.)

 

[dvvv]

I was unsure what to do with N1 and f, but I guess it makes sense that the torque is zero since there is no distance. The diagram also helps.

torque due to mg = torque due to N2
I said d was the length of the ladder.
1/2*d*mg*sin(theta) = d*1/2*mg*cos(theta)
then I get tan(theta) = 1
so theta = 45
So if theta is less than 45 the ladder slips.

I'm not sure if I used cos and sin in the right place. I think sin is for vertical, that's why I used it for the force on mg.

Thanks for your help.

 

[SammyS]

Define θ.

The angle the ladder makes with the horizontal? OR is it the angle the ladder makes with the vertical?

 

[dvvv]

With the horizontal, is what I thought.

 

[SammyS]

With the horizontal, is what I thought.

Then your sin & cos should be switched.

 

[dvvv]

mg is vertical and N2 is horizontal, that's why I picked what I did. Clearly I'm not looking at it the right way. I'm not sure how you work it out.

 

[SammyS]

What is the moment arm in each case and/or how is torque defined?

 

[cupid.callin]

@ cupid.callin.

I see that our responses were ~2 minutes apart. They compliment each other quite well.

Looking at this problem reminds me of that ladder problem in that list of questions you posted a while back. Usually the wall doesn't produce much friction, so I think the ladder's bottom is more likely to "kick out" when a person is near the top, rather than near the bottom. (The person on the ladder may be viewed as shifting the C.M. up or down the ladder.)

Hi Sammy

Yes you are right. While i was doing that chapter i encountered quite a complex numerical problem and unknowingly i solved the ladder question i posted while doing that problem.
But i still haven't been able to answer that weight balance problem.

@ dvvv

magnitude of Torque about a point is defined as force multiplied by the perpendicular distance of line of force from the point

for example like this:

Here torque, τ = Fd

Thats why Sammy asked you to switch your sin and cos

but remember that this doesn't tell the direction

for direction use:

$$\vec{\tau} = \vec{r} X \vec{F}$$

 

[dvvv]

Ok, I get it now, thanks.