Ladder with 2 forces of friction and a person climbing (statics)

[natasha13100]

1. Homework Statement
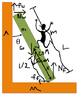
A uniform ladder of mass m and length L rests against the wall as shown. The wall is frictionless. The coefficient of static friction between the floor and the ladder is μ. The ladder makes the angle θ with the wall. How far along the ladder can a person of mass m climb before the ladder begins to slide?

2. Homework Equations
f(friction)≤μN(normal force)
t(torque)=r(moment arm)Fsinθ
G=mg

3. The Attempt at a Solution
FBD is attached

because the ladder is not moving
t=-mgLsinθ/2+NfLsinθ-μNfLcosθ-mg(L-x)sinθ=0
Fx=Nw-ff=0
Fy=Nf+fw-2mg=0

Solve t for Nf
NfLsinθ-μNfLcosθ=mgLsinθ/2+mg(L-x)sinθ
Nftanθ-μNf=mgtanθ/2+mg(L-x)tanθ/L
Nf=mg(1/2+(L-x)/L)/(1-mu/tanθ)

When θ is at its maximum without the ladder slipping, f=μN.
ff=μmg(1/2+(L-x)/L)/(1-mu/tanθ)
Solve Fxfor Nw
Nw=μmg(1/2+(L-x)/L)/(1-mu/tanθ)
Also fw=μ²mg(1/2+(L-x)/L)/(1-mu/tanθ)

Solve Fy for x.
mg(1/2+(L-x)/L)/(1-mu/tanθ)+μ²mg(1/2+(L-x)/L)/(1-mu/tanθ)-2mg=0
3/2-x/L=2(1-μ/tanθ)/(1+μ²)
x/L=3/2-2(1-μ/tanθ)/(1+μ²)
x=L(3/2-2(1-μ/tanθ)/(1+μ²))

 

[ehild]

The wall is frictionless, so [STRIKE]ff=0[/STRIKE]. fw=0
Edit: It is fw that is zero
ehild

 

[sonnyfab]

There is friction in the floor, so ff is not 0. However, fw should be 0 as the wall is frictionless.

Dr Peter Vaughan
BASIS Peoria Physics

 

[natasha13100]

Okay, I feel really dumb. I mixed together this problem with the one below it when I was working. This is a lot easier.
Solve for Nf using Fy.
Nf=2mg
Solve for x using t.
-mg(L-x)sinθ-mgLsinθ/2+2mgLsinθ-2μmglcosθ=0
-mgxsinθ+mgLsinθ/2-2μmglcosθ=0
mgxsinθ=2μmglcosθ-mgLsinθ/2
xtanθ=2μL-Ltanθ/2
x=2μL/tanθ-L/2
Please correct me if I'm wrong.

 

[ehild]

It is correct now.

ehild

 

[Kyle Newman]

Where are you getting an angle to plug into your equations? The question just says that it touches the wall at angle theta.