member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
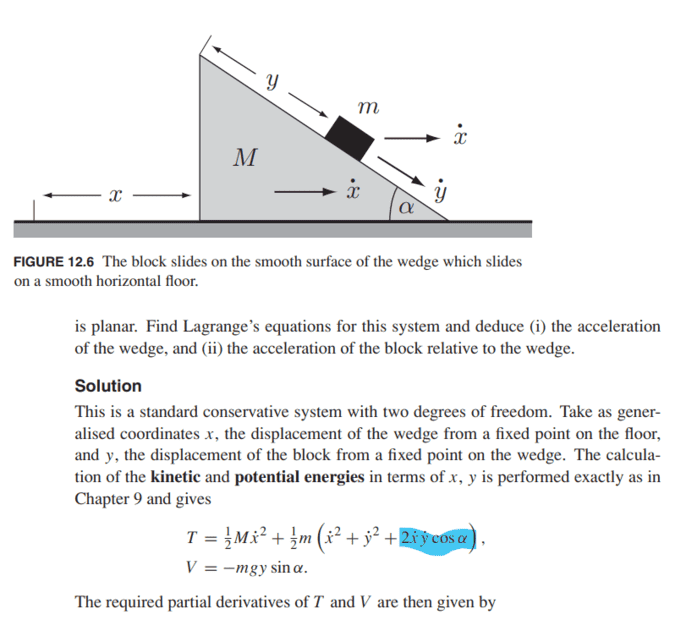
Does someone please know where the term highlighted in blue came from?
Thanks!
Does someone please know where the term highlighted in blue came from?
Thanks!