SUMMARY
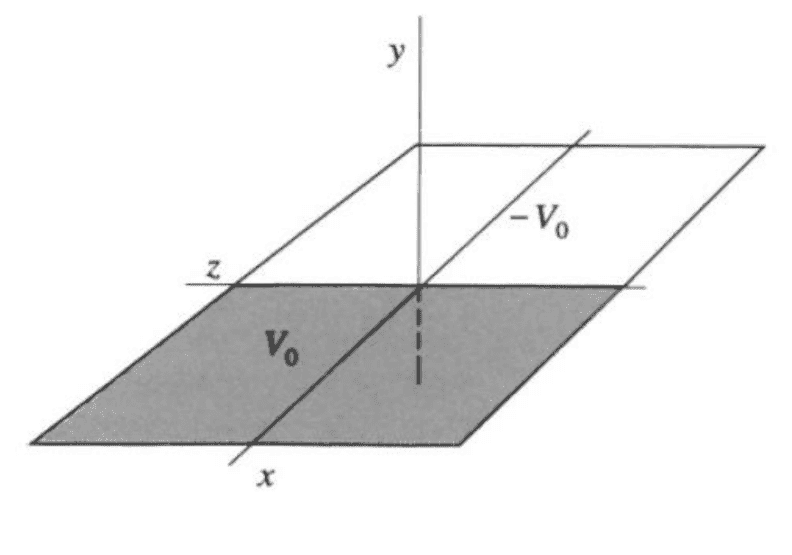
This discussion focuses on solving Laplace's Equation with specified boundary conditions using separation of variables and Green's functions. The boundary conditions identified are that as x approaches infinity, V equals V0, and as x approaches negative infinity, V equals -V0. The participants emphasize the importance of defining boundary conditions accurately and suggest breaking integrals into parts for different regions. The use of integral tables is recommended for evaluating the resulting expressions.
PREREQUISITES
- Understanding of Laplace's Equation in electrostatics
- Familiarity with boundary conditions in potential problems
- Knowledge of Green's functions and their application in physics
- Proficiency in separation of variables in Cartesian coordinates
NEXT STEPS
- Study the application of Green's functions in solving boundary value problems
- Learn about integral tables and their use in evaluating complex integrals
- Explore advanced techniques for solving Laplace's Equation in different coordinate systems
- Investigate the implications of boundary conditions on potential functions in electrostatics
USEFUL FOR
Physics students, particularly those studying electrostatics and boundary value problems, as well as educators and researchers looking to deepen their understanding of Laplace's Equation and its applications.