- #1
madilyn
- 13
- 0
Let's say I'm applying electrical currents to a certain part of a human test subject and measuring certain deflections in his heart readings during this period. Before I increase the electrical currents, which could be dangerous, I'm interested to see if the changes in electrical currents are causing ("leading") the fluctuations in heart readings.
Because of the nature of the measuring devices, the heart readings have a discrete sample space while the electrical current readings have a continuous sample space.
My question is: Is there a suitable lead-lag test for these two variables?
My planned mode of attack is to use the Granger causality test. I will take the differences in log currents and differences in log deflections: and because these currents (mA) and deflections are very small, they are valid approximations of the change in current and change in deflection. This also seems to meet the stationarity requirement of the Granger causality test.
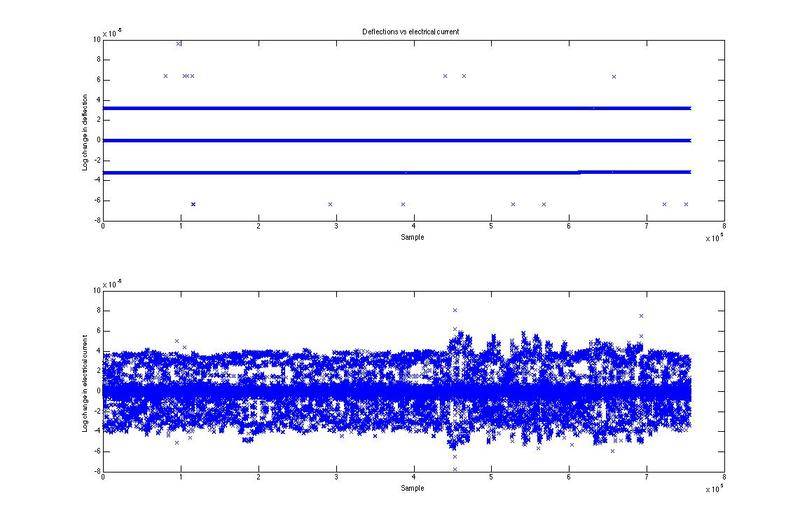
Now, I fit a VAR(p) model with suitable number of lags [itex]p[/itex] based on the Bayesian information criterion and toss it into the Granger casuality test. (http://en.wikipedia.org/wiki/Granger_causality) My only concern is that I'm not applying this test correctly because of certain invalid assumptions. Any thoughts?
Thanks!
Because of the nature of the measuring devices, the heart readings have a discrete sample space while the electrical current readings have a continuous sample space.
My question is: Is there a suitable lead-lag test for these two variables?
My planned mode of attack is to use the Granger causality test. I will take the differences in log currents and differences in log deflections: and because these currents (mA) and deflections are very small, they are valid approximations of the change in current and change in deflection. This also seems to meet the stationarity requirement of the Granger causality test.
Now, I fit a VAR(p) model with suitable number of lags [itex]p[/itex] based on the Bayesian information criterion and toss it into the Granger casuality test. (http://en.wikipedia.org/wiki/Granger_causality) My only concern is that I'm not applying this test correctly because of certain invalid assumptions. Any thoughts?
Thanks!