Left hand and right hand limits

[grace77]

Problem statement
What is the left hand and right hand limit of 1/x^2 -4 at its vertical asymptote?

Revelant equations
None

Attempt at a solution
It's vertical asymptote are 2 and -2.

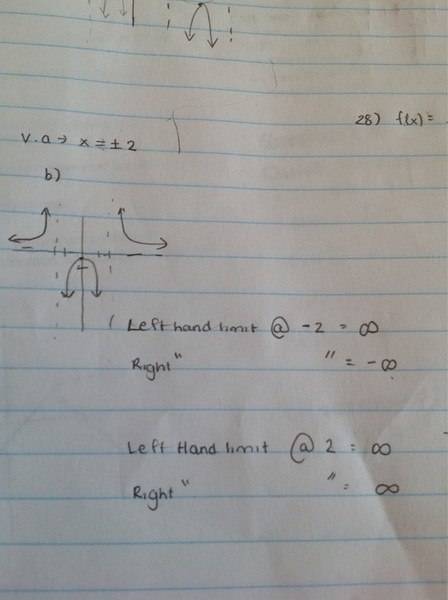
I have attached my work . I understand it however at the back of the book it says the left hand limit at 2 is negative infinity. That I don't understand as if you look at the graph I have drawn the left hand limit at 2 is going in a positive direction.

Does anyone have any insight on this? Thank you!

 

[BruceW]

your graph is correct. but your written answer does not match the graph. The left-hand limit at 2 should be where the curve is going, when x is just left of 2. So when the curve is just before x=2, where is the curve going towards: -infinity or +infinity?

 

[grace77]

your graph is correct. but your written answer does not match the graph. The left-hand limit at 2 should be where the curve is going, when x is just left of 2. So when the curve is just before x=2, where is the curve going towards: -infinity or +infinity?

Oh so you look at it before the curve : in this case it is heading downwards therefore it's a negative infinity

 

[BruceW]

yep. you look at the curve just left of the x value you are interested in. p.s. it's better to write the equation as 1/(x^2-4) instead of 1/x^2 -4 since this is confusing without the bracket. You might even lose marks if you hand it in without the bracket. I'm sure I've done that in the past. Although, on paper it is more obvious, since you can put it all under the division sign.

 

[grace77]

yep. you look at the curve just left of the x value you are interested in. p.s. it's better to write the equation as 1/(x^2-4) instead of 1/x^2 -4 since this is confusing without the bracket. You might even lose marks if you hand it in without the bracket. I'm sure I've done that in the past. Although, on paper it is more obvious, since you can put it all under the division sign.

Ok thank you Bruce! You are a lifesaver!

 

[BruceW]

haha, glad to help. But I'll get a big ego if you say things like that!