Physical_Fire said:
Yeah I understand that
@PeroK. But how do I solve it mathematically dy/dt (x,t) = -v * f'(x-vt)? Since it's a sin graph, dy/dt (x,t) = -v * cos(x-4pi). But it doesn't give me the correct graph. Why and how do I get the correct graph mathematically?
If we go back to this. We start with the wave equation:
$$y(x, t) = \sin(x - vt)$$This cannot be represented on a 2D graph. The best visualisation is an animation of a series of 2D graphs of ##y## against ##x## at each time ##t##. The first question is whether the wave is moving to the right or left? Let's assume that ##v## is positive.
First, we can see that at ##t = 0## we have:$$y(x, 0) = \sin(x)$$Now, what does the graph look like after some small time interval ##\Delta t##? Initially we have
$$y(0,0) = 0 \ \text{and} \ \ y(\frac \pi 2, 0) = 1$$At time ##\Delta t##, we have:
$$y(v\Delta t, \Delta t) = 0 \ \ \text{and} \ \ y(\frac \pi 2 + v\Delta t, \Delta t) = 1$$And we can see that the point on the wave where ##y = 0## has moved to the right by a distance ##v\Delta t## and the initial peak at ##x = \frac \pi 2## has also moved to right by the same distance. This is what we mean by the wave moving to the right with speed ##v##.
Technically, however, no points are moving to the right. Instead, each point on the wave is moving up and down. We can look at the points at ##x =0## and ##x = \frac \pi 2## and describe their motion over time. We have:
$$y(0, t) = \sin(-vt) \ \ \text{and} \ \ y(\frac \pi 2, t) = \sin(\frac \pi 2 - vt)$$And the motion of these points is:
$$\frac{dy}{dt}(0, t) = -v\cos(-vt) \ \ \text{and} \ \ \frac{dy}{dt}(\frac \pi 2, t) = -v\cos(\frac \pi 2 - vt)$$When we plot these motions on a graph, they have the same shape as the wave - the cosine is just the sine with a different phase. The important question here is the direction of motion of these points at time ##t = 0##:
$$\frac{dy}{dt}(0, 0) = -v \ \ \text{and} \ \ \frac{dy}{dt}(\frac \pi 2, 0) = 0$$And we can see that at time ##t =0## the point at the origin is
moving down (at the maximum speed) and the point at ##x = \frac \pi 2## is instantaneously at rest. And, indeed, this point must move down immediately after ##t = 0##.
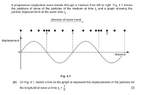
That's why if we draw a graph of the point X, which is a zero point on the wave to the left of a peak, it is initially moving down. Likewise, a zero point on the graph that is to the left of a trough will initially be moving up. In general, points
behind a peak are moving
down; and, points
in front of a peak are moving
up. This should make sense if you think of the wave coming through and lifting up points and dropping them back down again.
Another way to look at this is to consider a frame of reference in which the wave is at rest. I.e. a reference frame moving to the right at speed ##v##. In this frame, the points on the x-axis are moving to the left with speed ##v## and following the wave in the reverse direction, as it were. E.g. the point X is headed for a trough and must be initially moving down.