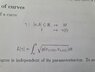A Levi-Civita Connection & Length of Curves in GR

[Blub]

I am studying GR and I have these two following unresolved questions up until now:

The first one concerns the Levi-Civita connection. There are two conditions which determine the affine connections. The first one is that the connection is torsion-free (which is true for space-time and comes from experiment), the second one is that the parallel transport is an isometry/ the metric is invariant at each point on the manifold. My question is that why can we impose this 2. condition?

My 2. question is about the length of curves on a manifold, which is given by the formula in the pic I attached.

g is the metric tensor and v the tangent vector of gamma at the point gamma of t.

This is maybe a dumb question, but wouldn't this mean by this formula that the length of a curve depends on how fast we move through the curve? Or maybe my understanding of a tangent vector is wrong...

Any help would be greatly appreciated.

 

[etotheipi]

My 2. question is about the length of curves on a manifold, which is given by the formula in the pic I attached.

g is the metric tensor and v the tangent vector of gamma at the point gamma of t.

This is maybe a dumb question, but wouldn't this mean by this formula that the length of a curve depends on how fast we move through the curve? Or maybe my understanding of a tangent vector is wrong...

I don't know the answer to the first question but for the second, if $v(t) = d\gamma / dt$ is a tangent vector to the path at parameter $t$, then like it says in your book the length of the path will be$$L[\gamma] = \int_{t_1}^{t_2} dt \sqrt{g(v,v)}$$or if you represent the path in some coordinates $x^{\mu}(t)$,$$L[\gamma] = \int_{t_1}^{t_2} dt \sqrt{g_{\mu \nu} \frac{dx^{\mu}}{dt} \frac{dx^{\nu}}{dt}}$$but you could also change the parameterisation of the path to $\tilde{\gamma} : [\tilde{t}_1, \tilde{t}_2] \rightarrow M$, i.e. changing 'how quickly' you go along the path, so that your new tangent vector is $\tilde{v}(\tilde{t}) = d\tilde{\gamma} / d\tilde{t}$. Using the chain rule,$$L[\tilde{\gamma}] = \int_{\tilde{t}_1}^{\tilde{t}_2}\frac{dt}{d\tilde{t}} d\tilde{t}\sqrt{g_{\mu \nu} \frac{dx^{\mu}}{d\tilde{t}} \frac{dx^{\nu}}{d\tilde{t}} \left( \frac{d\tilde{t}}{dt}\right)^2} = \int_{\tilde{t}_1}^{\tilde{t}_2} d\tilde{t}\sqrt{g_{\mu \nu} \frac{dx^{\mu}}{d\tilde{t}} \frac{dx^{\nu}}{d\tilde{t}} } = \int_{\tilde{t}_1}^{\tilde{t}_2}d\tilde{t} \sqrt{g(\tilde{v}, \tilde{v})} $$and in that way, the length of the path shouldn't depend on the parameter you choose.

 

[Ibix]

A slightly less rigourous way of stating what @etotheipi said is that the tangent vector is normalised (often to $c$, sometimes to 1 even in unit systems where $c\neq 1$), so its modulus isn't physically signficant. Changing your normalisation must then come out in the wash, which is what the maths above shows.

Regarding your first question, metric compatibility is a formal way of requiring that if I define a local Lorentz frame inside my free-falling spaceship then wait a while (parallel transporting my local frame along a geodesic) my frame definition remains a valid local Lorentz frame.

 

[Blub]

I don't know the answer to the first question but for the second, if $v(t) = d\gamma / dt$ is a tangent vector to the path at parameter $t$, then like it says in your book the length of the path will be$$L[\gamma] = \int_{t_1}^{t_2} dt \sqrt{g(v,v)}$$or if you represent the path in some coordinates $x^{\mu}(t)$,$$L[\gamma] = \int_{t_1}^{t_2} dt \sqrt{g_{\mu \nu} \frac{dx^{\mu}}{dt} \frac{dx^{\nu}}{dt}}$$but you could also change the parameterisation of the path to $\tilde{\gamma} : [\tilde{t}_1, \tilde{t}_2] \rightarrow M$, i.e. changing 'how quickly' you go along the path, so that your new tangent vector is $\tilde{v}(\tilde{t}) = d\tilde{\gamma} / d\tilde{t}$. Using the chain rule,$$L[\tilde{\gamma}] = \int_{\tilde{t}_1}^{\tilde{t}_2}\frac{dt}{d\tilde{t}} d\tilde{t}\sqrt{g_{\mu \nu} \frac{dx^{\mu}}{d\tilde{t}} \frac{dx^{\nu}}{d\tilde{t}} \left( \frac{d\tilde{t}}{dt}\right)^2} = \int_{\tilde{t}_1}^{\tilde{t}_2} d\tilde{t}\sqrt{g_{\mu \nu} \frac{dx^{\mu}}{d\tilde{t}} \frac{dx^{\nu}}{d\tilde{t}} } = \int_{\tilde{t}_1}^{\tilde{t}_2}d\tilde{t} \sqrt{g(\tilde{v}, \tilde{v})} $$and in that way, the length of the path shouldn't depend on the parameter you choose.

That makes sense. I think I was also comparing tangent vectors living in different tangent spaces in my mind and got confused about the notion of velocity on a manifold. Thank you for your help.

 

[ChinleShale]

I believe that in order for a local Lorentz frame to exist at each point, the affine connection must be both torsion free and metric compatible. Such a connection is a Levi-Civita connection by definition.

A connection that is torsion free but not necessarily compatible with a metric still has a local frame -called normal coordinates - in which the Christoffel symbols vanish at the central point of the coordinate system. If the torsion is not zero at the central point then the Christoffel symbols can not vanish. Metric compatibility will not insure this. There are metric compatible connections that are not torsion free.

It is also true that in a Levi-Civta connection that the first partial derivatives of the metric tensor components are zero at the central point of a normal coordinate system. What is the physical significance of this condition?

 

[Ibix]

What is the physical significance of this condition?

I think non-zero first partial derivatives of the metric means that there are inertial forces present. In the context of gravitation this means that we feel gravity in the every day sense of "let go of a ball and it falls" (e.g., in Schwarzschild coordinates $\partial_r g\neq 0$). So, that they vanish in a local Lorentz frame means that such frames are inertial (MTW seems to regard this as another way of describing metric compatibility).

 

[pervect]

There is at least one theory of gravity in which the metric is not torsion free, Einstein-Cartan theory. See for instance https://en.wikipedia.org/w/index.php?title=Einstein–Cartan_theory&oldid=965218745. Wiki states that the theory has a locally gauged Lorentz symmetry. However, the theory is normally indistinguishable from GR. Only in extreme conditions where quantum spin becomes important does it differ experimentally. Einstein-Cartan theory gets rid of the singularities due to gravitational collapse, replacing them with a "bounce", and it solves some problems GR has when trying to do semi-classical approximations involving particles with spin.

 

[vanhees71]

I think that the extension of GR to Einstein-Cartan theory is necessary given that obviously there are elementary particles with spin 1/2 (quarks and leptons). This of course doesn't contradict the great empirical success of GR since it's tested of course only on (very) macroscopic systems, where spin doesn't play too much of a role since the usual thermal systems are randomized concerning the spins. The other relevant field is of course the electromagnetic one, and this also doesn't imply torsion. I think that's the reason, why standard GR is so successful (in some respects at very high precision as from pulsar-timing observations concerning the PPN parameters, which AFAIC all are with very high significance compatible to the GR values).

 

[strangerep]

I think that the extension of GR to Einstein-Cartan theory is necessary given that obviously there are elementary particles with spin 1/2 (quarks and leptons).

Why "necessary"?

Roy Kerr showed [Ref 1] that, in a Lorentz-covariant improvement of the Einstein-Infeld-Hofman method for extracting equations of motion for test particles from the EFE, there are, at lowest order, additional constants that can be identified with intrinsic spin and a dipole moment of the particle's rest mass.
The classical equations of angular momentum also emerge from the analysis.

Ref 1:

R. P. Kerr,
The Lorentz-Covariant Approximation Method in General Relativity. - I
Nuovo Cimento, vol XIII, no 3, p469 (1959).

(See also his 2nd paper that performs the analysis at the next higher order, and a 3rd paper incorporates an electromagnetic stress tensor in the EFE.)

 

[vanhees71]

Interesting, but I thought to get a consistent theory of Dirac fields in curved spacetime you need necessarily a spacetime with torsion, at least if you use the gauge approach (i.e., making Lorentz invariance of SR local).