akaliuseheal
- 53
- 8
Homework Statement
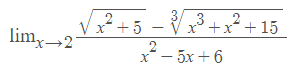
Can I use L'Hopital's rule here. What I get as a solution is -30/-27 while in the notebook,
without using the L'Hopital's rule the answer is -(2/27)
The attempt at a solution
The derivatives i get are:
x/(x2+5)½
(3x2+2x)/3(x3+x2+15)⅓
2x-5
½ and ⅓ are there because it's easier for me to write it here on this forum like that instead of sqrt.
So..
limx→2( ( x/(x2+5)½ - (3x2+2x)/3(x3+x2+15)⅓ ) / 2x-5 )
Image:
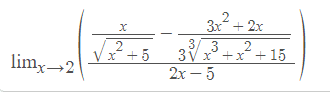
x = 2 ⇒ -30/-27 (1.11)
Could't find software online to verify the solution (symbolab gave no answer) so here I am.
But symbolab did gave me the same answer as I got when I entered the expression from the second image.
Can I use L'Hopital's rule here. What I get as a solution is -30/-27 while in the notebook,
without using the L'Hopital's rule the answer is -(2/27)
The attempt at a solution
The derivatives i get are:
x/(x2+5)½
(3x2+2x)/3(x3+x2+15)⅓
2x-5
½ and ⅓ are there because it's easier for me to write it here on this forum like that instead of sqrt.
So..
limx→2( ( x/(x2+5)½ - (3x2+2x)/3(x3+x2+15)⅓ ) / 2x-5 )
Image:
x = 2 ⇒ -30/-27 (1.11)
Could't find software online to verify the solution (symbolab gave no answer) so here I am.
But symbolab did gave me the same answer as I got when I entered the expression from the second image.