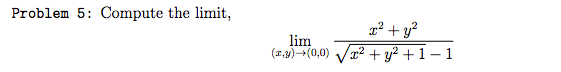Limit of ((x2+y2+1)1/2) - 1: Evaluate & Simplify

[Jamie2]

View attachment 2085

I got that the limit equals 0 by simplifying the denominator from:

((x²+y²+1)^1/2) - 1

to
((x² - (y+1)(y-1))^1/2) - 1

then
((x² - (y(1+1)(1-1))^1/2) - 1

and then evaluating the limit by plugging in 0, getting 0/-1=0

is this correct? is there a better way to do it?

 

[MarkFL]

I get a different result by converting to polar. This result is confirmed by W|A. So, I suggest using polar coordinates...what do you find?

 

[Jamie2]

Could you explain in more detail? I don't think I understand what you mean

 

[MarkFL]

Essentially, I used $x^2+y^2=r^2$ and the limit becomes:

$$\lim_{r\to0}\left(\frac{r^2}{\sqrt{r^2+1}-1} \right)$$

And then I rationalized the denominator. You could also at this point use L'Hôpital's Rule.