Linear Momentum Homework: 6kg Ball Hits Wall at 4.96 m/s

[Jake4]

Homework Statement

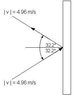
A 6kg ball hits a wall going 4.96 m/s at an angle of 32.2 degrees from perpendicular. It is in contact with the wall for .134 seconds. What is the average Force exerted by the wall.

Homework Equations

P=MV

(delta)P = FT

The Attempt at a Solution

I have a hunch that the software online is looking for the incorrect answer. This problem is so entirely simple, and I've solved many like it. however, my professor hasn't gotten back to me, and I'm going crazy.

We actually had an exam last week, and this problem was a bonus (because we hadn't really started linear momentum at the time) and I got it correct...


My solution was simply P=MV, so (6kg)(4.96cos(32.2)) = P Then, given P=FT I took the resulting linear momentum and divided it by the .134 seconds. I don't have my calculator right here, but it gave me something like 187 N. I tried that as well as the same answer negative, and both were incorrect.

I feel like either the computer is incorrect, or I'm missing something VERY fundamental. I apologize in advance if this turns out to be a dumb fix, I was working all night smoothly on my physics stuff, and came to a screeching halt on one of the simplest problems on the sheet... you can imagine my frustration >.<


Thanks!

 

[cepheid]

The impulse is equal to the change in momentum. To get the change in momentum, you have to subtract the initial momentum from the final momentum. The final momentum is the momentum the ball has once it loses contact with the wall.

 

[Jake4]

So then it should be essentially.. 6(4.96cos(32.2)) to find P... it comes off the wall at the same angle and velocity, so P-final = -P-initial.

So it would essentially be -2(25.2) = F(.134)
F = -376 N?

 

[cepheid]

So then it should be essentially.. 6(4.96cos(32.2)) to find P... it comes off the wall at the same angle and velocity, so P-final = -P-initial.

So it would essentially be -2(25.2) = F(.134)
F = -376 N?

Does it say in the problem that it comes off the wall at the same angle and speed?

 

[Jake4]

oh sorry about that, yes that was given. Same velocity and same angle.

 

[cepheid]

Okay, so since the ball's momentum goes from p to -p, the change is -2p.

I'm not sure why you're applying the cosine factor. That is only the x-component of the momentum. Use the change in total momentum.

 

[Jake4]

Because the momentum in the y direction doesn't change? I was taught that linear momentum is a vector quantity.

 

[cepheid]

Because the momentum in the y direction doesn't change?

Yes, it does. It is the negative of what it was before the collision. Try drawing a picture of the incoming momentum vector and its resolved x and y components, taking care with the directions of all the arrows. Now draw the outgoing vector resolved into components.

I was taught that linear momentum is a vector quantity.

I was not trying to suggest otherwise. But you're just interested in computing the magnitude of the force. The direction follows automatically from the impulse-momentum theorem, since FΔt = Δp (I use boldface to represent vectors). And Δp just points in the opposite direction of p_init i.e. it has been rotated by 180°. This is automatically taken care of by the negative sign here:

Δp = -2mv_init

Therefore, the magnitude of the force is F = (2mv_init)/Δt

and its direction is 180° away from the direction of the incoming velocity.

EDIT: You could resolve Δp into x and y components and you'd get the same answer for both magnitude and direction, but this is easier.

 

[gneill]

Please forgive me for butting in at this late date, but does the following diagram more or less depict the scenario under consideration?

 

[Jake4]

yes ^^ it does. as you can see in the diagram, the y momentum does not reverse, but stays constant. The only momentum that changes by 180 degrees is the x momentum.

 

[gneill]

Okay. So it looks as though you were proceeding on the right lines when you considering the components. Taking the vertical direction as y, and the horizontal as x, the initial and final momentum vectors are:

p1 = mvcos(θ)i + mvsin(θ)j

p2 = -mvcos(θ)i + mvsin(θ)j

so that

Δp = p2 - p1 = -2mvcos(θ)i

and

F = Δp/Δt

Plug in your values and you've got your force vector.

 

[cepheid]

So then it should be essentially.. 6(4.96cos(32.2)) to find P... it comes off the wall at the same angle and velocity, so P-final = -P-initial.

I should point out that these statements are not at all consistent with the diagram. It comes off the wall with an angle that is the negative of what it was before (ie it is reflected across the normal). Also it is not true that p_final = -p_initial.

It was on the basis of your above statements that I assumed that the ball simply reversed direction.

 

[Jake4]

Oh, well I don't mean to cause a disagreement, but from the same statements he got that diagram.

I certainly could have explained it better, sorry about that.

but yes cepheid, that seems to work intuitively as well as numerically :)

thanks!