Local Basis in Topology .... Definitions by Croom and Singh .... ....

[Math Amateur]

TL;DR Summary

I need help in order to investigate two apparently different definitions of a local basis in a topological space ...

Fred H. Croom (Principles of Topology) and Tej Bahadur Singh (Elements of Topology) define local basis (apparently) slightly differently ...

Croom's definition reads as follows:

... and Singh's definition reads as follows:

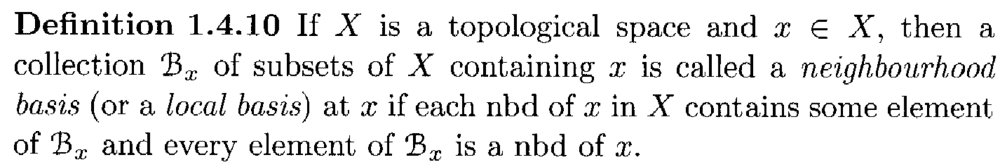
The two definitions appear different ... ...

Croom requires that each open set containing a contains a member of $\mathcal{B}_a$ ...

... while Singh requires each nbd of x to contain some element of a member of $\mathcal{B}_x$ ... and one notes that the open set (necessarily) contained in the nbd would necessarily intersect with a member of $\mathcal{B}_x$ ... it would not necessarily contain the member of $\mathcal{B}_x$ ... so I see the definitions as different ...

Is that correct?

If the definitions are indeed different ... which is the more common definition ...?

Further ... are their significant implications for further theory built on these definitions ...?Help will be much appreciated ... ...

Peter=======================================================================================It may help Physics Forums readers of the above post to have access to Singh's definitions of a neighborhood (nbd) ...
... so I am providing the same ... as follows:

Hope that helps ...

Peter

 

[fresh_42]

Neighborhood and open set are synonyms. Neighborhood is a bit more common, as it emphasizes that its local nature, whereas open set only says within the topology. But as he always adds open set which contains a (or x), the local nature is added via this sub-clause. And in both cases, such an open set or neighborhood of a (or x), has to entirely contain some member of the basis.

It is always the same trick: "open means something smaller and also open must be within". And a local basis means, that this "open within" can be chosen from the local basis, which is a certain set of open sets, i.e. a subset of $\mathcal{P(T)}$.

The two definitions are not only equivalent, they are identical; just phrased differently.

 

[member 587159]

Neighborhood and open set are synonyms.

Given the definition the OP gave, they are not. $[-1,1]$ is a neighborhood of $0$ in the usual topology but not open.

 

[Math Amateur]

Neighborhood and open set are synonyms. Neighborhood is a bit more common, as it emphasizes that its local nature, whereas open set only says within the topology. But as he always adds open set which contains a (or x), the local nature is added via this sub-clause. And in both cases, such an open set or neighborhood of a (or x), has to entirely contain some member of the basis.

It is always the same trick: "open means something smaller and also open must be within". And a local basis means, that this "open within" can be chosen from the local basis, which is a certain set of open sets, i.e. a subset of $\mathcal{P(T)}$.

The two definitions are not only equivalent, they are identical; just phrased differently.

Thanks fresh_42 ...

But surely (given Singh's definition ... see my post ... ) nbd and open set are not synonyms and the two definitions are slightly different ...

So I am still wondering about the implications of the differences ...

Peter

 

[fresh_42]

Given the definition the OP gave, they are not. $[-1,1]$ is a neighborhood of $0$ in the usual topology but not open.

Oops, I haven't read as far.

However, Peter (@Math Amateur), this doesn't change the basic idea. I know neighborhoods as open sets, but of course they can likewise be defined as sets which contain an open set (plus the point they are neighboring). Just pass to this open set instead, let's call it open neighborhood$^* \subseteq$ neighborhood.

This a small technical difference, not a basic one.

 

[Math Amateur]

Given the definition the OP gave, they are not. $[-1,1]$ is a neighborhood of $0$ in the usual topology but not open.

Thanks Math_QED ...

What can be said about the implications for further theory ... for example for propositions/theorems about first countable spaces ...

Peter

 

[fresh_42]

Thanks Math_QED ...

What can be said about the implications for further theory ... for example for propositions/theorems about first countable spaces ...

Peter

There are none. See my post above. You can always pass to U=nbd$^*$ and get the same situation.

 

[Math Amateur]

Oops, I haven't read as far.

However, Peter (@Math Amateur), this doesn't change the basic idea. I know neighborhoods as open sets, but of course they can likewise be defined as sets which contain an open set (plus the point they are neighboring). Just pass to this open set instead, let's call it open neighborhood$^* \subseteq$ neighborhood.

This a small technical difference, not a basic one.

Thanks fresh_42 ,,,

In my original post I wrote ...

" ... ... Croom requires that each open set containing a contains a member of $\mathcal{B}_a$ ...

... while Singh requires each nbd of x to contain some element of a member of $\mathcal{B}_x$ ... and one notes that the open set (necessarily) contained in the nbd would necessarily intersect with a member of $\mathcal{B}_x$ ... it would not necessarily contain the member of $\mathcal{B}_x$ ... so I see the definitions as different ... ... "

Was my analysis correct?

Peter

 

[fresh_42]

The definitions are formally different:

In the first definition we have $a \in B_a \subseteq O$ all open.

In the second definition we have $x \in U_1 = nbd_1^* \subseteq B_x \subseteq nbd_2$ where $nbd_2$ implies there is another open set $x\in U_2 \subseteq nbd_2$.

They are technically the same thing, such as if you start natural numbers at $1$ or $0$. It only makes things more complicated, if you allow neighborhoods or basis sets to be not open. All of them have a smaller open set within. The first definition directly uses these smaller open sets, the second one only makes things less obvious.

The advantage of the second one is, that you don't have to care about openness when it isn't needed. But I doubt that this weighs heavier than the clarity of the first definition. It's like: some authors automatically mean $1\in R$ if they speak of a ring, others don't.

Edit: There is one major difference I just recognized. Whereas in definition 1 the basis sets have to be within an open set, there is not necessarily an open set between a basis set and a neighborhood in definition 2. The open set $U_2$ which is required in definition 2 doesn't need to contain $B_x$.

I would call the first definition local basis (open sets) and the second neighborhood basis just to distinguish them - keeping in mind that neighborhoods here don't have to be open, they only need to contain an open set.

Topology is a mess. I should stop answering questions about it ...

 

[member 587159]

I'll try to add my two cents as well.

Croom's definition asks that a neighborhood basis consists of open sets containing the fixed point while the other definition allows neighborhoods of this fixed point, so these mustn't be necessarily open.

So, strictly speaking there is a difference between both definitions. Clearly if you have a neighborhood basis consisting only of open sets (Croom's definition), this is a neighborhood system in the sense of the other definition. So one implication holds, the other one doesn't.

At first, having these two different definitions might seem problematic but it actually isn't for the following reason, which I leave as an exercise for you:

If you have a neighborhood system in the sense of Singh's definition, then there exists also a neighborhood system in the sense of Croom's definition (and you can choose this with cardinality equal or smaller than the neighborhood system you start with).

 

[Math Amateur]

I'll try to add my two cents as well.

Croom's definition asks that a neighborhood basis consists of open sets containing the fixed point while the other definition allows neighborhoods of this fixed point, so these mustn't be necessarily open.

So, strictly speaking there is a difference between both definitions. Clearly if you have a neighborhood basis consisting only of open sets (Croom's definition), this is a neighborhood system in the sense of the other definition. So one implication holds, the other one doesn't.

At first, having these two different definitions might seem problematic but it actually isn't for the following reason, which I leave as an exercise for you:

If you have a neighborhood system in the sense of Singh's definition, then there exists also a neighborhood system in the sense of Croom's definition (and you can choose this with cardinality equal or smaller than the neighborhood system you start with).

Thanks again for your help Math_QED ...

You write:

" ... ... If you have a neighborhood system in the sense of Singh's definition, then there exists also a neighborhood system in the sense of Croom's definition ... ..."

But ... how can this be ... for as I write in my original post ...

" ... ... Croom requires that each open set containing x contains a member of $\mathcal{B}_x$ ...

... ... while Singh requires each nbd of x to contain some element of a member of $\mathcal{B}_x$ ... and one notes that the open set (necessarily) contained in the nbd would necessarily intersect with a member of $\mathcal{B}_x$ ... it would not necessarily contain the member of $\mathcal{B}_x$ ... "

In short the open sets within Singh's neighborhoods do not contain a member of $\mathcal{B}_x$ ... an essential requirement of Croom's definition ...

Can you comment and clarify ...

Peter

 

[Math Amateur]

The definitions are formally different:

In the first definition we have $a \in B_a \subseteq O$ all open.

In the second definition we have $x \in U_1 = nbd_1^* \subseteq B_x \subseteq nbd_2$ where $nbd_2$ implies there is another open set $x\in U_2 \subseteq nbd_2$.

They are technically the same thing, such as if you start natural numbers at $1$ or $0$. It only makes things more complicated, if you allow neighborhoods or basis sets to be not open. All of them have a smaller open set within. The first definition directly uses these smaller open sets, the second one only makes things less obvious.

The advantage of the second one is, that you don't have to care about openness when it isn't needed. But I doubt that this weighs heavier than the clarity of the first definition. It's like: some authors automatically mean $1\in R$ if they speak of a ring, others don't.

Edit: There is one major difference I just recognized. Whereas in definition 1 the basis sets have to be within an open set, there is not necessarily an open set between a basis set and a neighborhood in definition 2. The open set $U_2$ which is required in definition 2 doesn't need to contain $B_x$.

I would call the first definition local basis (open sets) and the second neighborhood basis just to distinguish them - keeping in mind that neighborhoods here don't have to be open, they only need to contain an open set.

Topology is a mess. I should stop answering questions about it ...

Thanks fresh_42 ...

I hope you do keep answering topology questions because I find your posts extremely informative and also extremely helpful ...

Thanks again for your help on this issue ...

Peter

 

[member 587159]

Suppose we have a nbh system $\mathcal{B}_x=\{B_i:i\in I\}$ as in Singh's definition.

Given $V_i\in \mathcal{B_x}$, let $W_i$ be an open set with $x\in W_i\subseteq V_i$. We show that $\{W_i:i\in I\}$ is a collection as in Croom' definition.

First note that by construction all sets in our new collection are open and contain $x$.

Let $O$ be an open containing $x$. In particular, $O$ is a nbh of $x$ and by Singh's definition, there is $i\in I$ with $V_i\subseteq O$. But then $W_i\subseteq O$ as well, so $\{W_i:i\in I\}$ satisfies Croom's definition.

Maybe I'm missing something? What do you think?

 

[Math Amateur]

Suppose we have a nbh system $\mathcal{B}_x=\{B_i:i\in I\}$ as in Singh's definition.

Given $V_i\in \mathcal{B_x}$, let $W_i$ be an open set with $x\in W_i\subseteq V_i$. We show that $\{W_i:i\in I\}$ is a collection as in Croom' definition.

First note that by construction all sets in our new collection are open and contain $x$.

Let $O$ be an open containing $x$. In particular, $O$ is a nbh of $x$ and by Singh's definition, there is $i\in I$ with $V_i\subseteq O$. But then $W_i\subseteq O$ as well, so $\{W_i:i\in I\}$ satisfies Croom's definition.

Maybe I'm missing something? What do you think?

I think your analysis is correct ... I cannot fault it ...

But now I cannot reconcile my analysis and yours ... they both seem correct yet are apparently contradictory ...

Can you clarify this situation ... =============================================================================
For convenience I repeat my analysis ...

" ... ... Croom requires that each open set containing x contains a member of $\mathcal{B}_x$ ...

... ... while Singh requires each nbd of x to contain some element of a member of $\mathcal{B}_x$ ... and one notes that the open set (necessarily) contained in the nbd would necessarily intersect with a member of $\mathcal{B}_x$ ... it would not necessarily contain the member of $\mathcal{B}_x$ ... "

In short the open sets within Singh's neighborhoods do not contain a member of $\mathcal{B}_x$ ... an essential requirement of Croom's definition ...

==============================================================================Hope that you can help further ...

Peter

 

[member 587159]

In short the open sets within Singh's neighborhoods do not contain a member of $\mathcal{B}_x$ ... an essential requirement of Croom's definition.

This seems false to me. An open set containing $x$ is also a neighborhood of $x$, so Singh's definition says that there is some $B_x$ contained in this open set.

Maybe you make a mistake even earlier. It's early here and the first thing I noticed.