Local Extrema of Quartic Function: Help Find (x, y) Points

[MarkFL]

Here is the question:

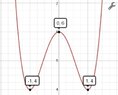
Can someone please help me find local maximum and local minimum?

Let f(x) = 2x^4 - 4x^2 + 6

Find the point(s) (x, y) at which f achieves:

local maximum - (?,?)
local minimum - (?,?)

can someone help me please
I get 1 and -1 but its wrong apparently

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello John,

We are given the function:

\(\displaystyle f(x)=2x^4-4x^2+6\)

And are asked to find the local extrema. In order to do this, we need to equate the first derivative to zero, and finct the critical values:

\(\displaystyle f'(x)=8x^3-8x=8x\left(x^2-1 \right)=8x(x+1)(x-1)=0\)

Hence, our critical values are:

\(\displaystyle x=-1,0,1\)

Observing that the roots here are all off multiplicity 1, and seeing that for $1<x$, we have:

\(\displaystyle f'(x)>0\)

we may then conclude that the sign of the derivative alternates across the 4 intervals made by dividing the real number line at the three critical values, hence we have:

\(\displaystyle f(x)\) increasing on \(\displaystyle (-1,0)\,\cup\,(1,\infty)\)

\(\displaystyle f(x)\) decreasing on \(\displaystyle (-\infty,-1)\,\cup\,(0,1)\)

Thus, by the first derivative test, we are led to conclude that we have the following:

Relative minima at \(\displaystyle \left(-1,f(-1) \right)=(-1,4)\) and \(\displaystyle \left(1,f(1) \right)=(1,4)\)

Relative maximum at \(\displaystyle \left(0,f(0) \right)=(0,6)\)

Here is a plot of the function and its relative extrema:

View attachment 2308