Locally inertial reference frame problem

[Pencilvester]

Hey PF, I am working on a problem set, and one of the problems is proving that the Christoffel symbols vanish at the origin of the coordinates $y^{\alpha}$ given by the coordinate transformation: $$y^\alpha (x) = x^\alpha - x^\alpha_{(0)} + \frac {1} {2} (x^\mu - x^\mu_{(0)} )(x^\nu - x^\nu_{(0)} ) \Gamma^\alpha_{(0) \mu \nu}$$ Where anything with a $(0)$ subscript is evaluated at some particular point.
Figuring out that $\frac {\partial y^{\alpha}} {\partial x^{\mu}} = \delta^{\alpha}_{\mu} + (x^{\lambda} - x^{\lambda}_{(0)}) \Gamma^{\alpha}_{(0) \mu \lambda}$ and that $\frac {\partial^2 y^{\alpha}} {\partial x^\mu \partial x^\nu} = \Gamma^{\alpha}_{(0) \mu \nu}$ was fairly straightforward, and I also know the transformation law for the Christoffel symbols, but I can't figure out how to find the inverse of the Jacobian—the $\frac {\partial x^\alpha} {\partial y^\mu}$’s. Here’s part of the solution (they use squiggles instead of $y$):

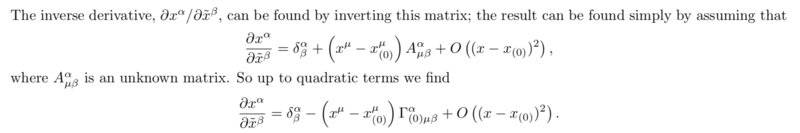
They’re clearly using a Taylor polynomial, but I don’t understand how to find that the unknown matrix $A^\alpha_{\mu \beta}$ ends up being $\Gamma^\alpha_{\mu \beta}$. I feel like I must be missing something super obvious. Would someone be so kind as to point out what I’m missing?

 

[Orodruin]

The chain rule.
$$
\newcommand{\dd}[2]{\frac{\partial #1}{\partial #2}}
\dd{x^\alpha}{y^\beta} \dd{y^\beta}{x^\gamma} = \dd{x^\alpha}{x^\gamma} = \delta^\alpha_\gamma.
$$
Insert the Taylor expansion into the above expression along with the coordinate transformation and identify $A$ from the linear term in $x - x_0$.

 

[Orodruin]

It should be noted that there is a significantly easier way of showing this. Just consider the geodesic equations in $x$ and show that they imply $\ddot y^\mu = 0$ at $x_0$.

 

[Pencilvester]

The chain rule.

Oh, duh. Yup, that would be the obvious thing I was missing.

It should be noted that there is a significantly easier way of showing this. Just consider the geodesic equations in $x$ and show that they imply $\ddot y^\mu = 0$ at $x_0$.

That definitely is much simpler and straightforward. Thanks!

 

[Orodruin]

Yup, that would be the obvious thing I was missing.

Sometimes you need to be pointed to the trees in the forest...