Steven Ellet
- 85
- 3
I am looking for a formula that will them me how many possible connections between 2 sets of objects.
Ex: 12 on left and 4 on right, how many possible states can it be in?
state one: top on left connected to top on right
state two: top on left connected to 2 on right
state three: top on left connected to top on right and 2 on right
state four: etc.
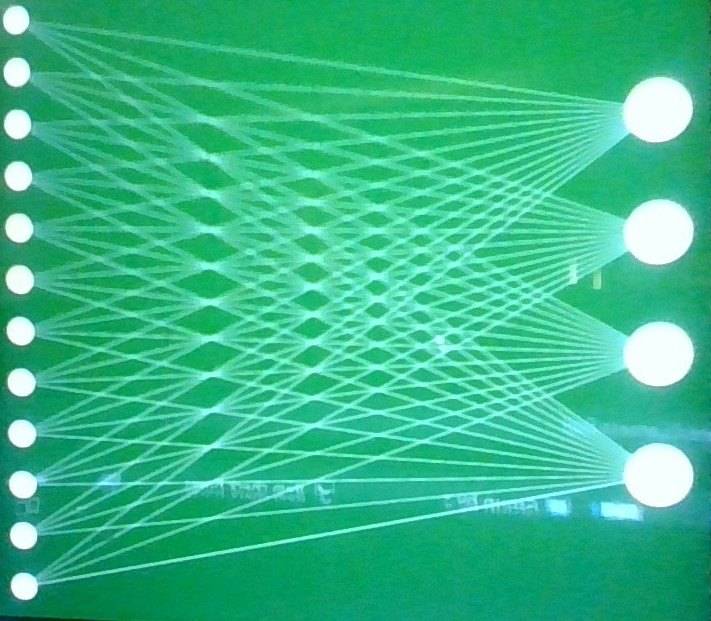
Ex: 12 on left and 4 on right, how many possible states can it be in?
state one: top on left connected to top on right
state two: top on left connected to 2 on right
state three: top on left connected to top on right and 2 on right
state four: etc.
Last edited by a moderator: