- #31
houlahound
- 907
- 223
Can a table of values for W be computed?
ie
z in cloum a, W(z) in colum b.
ie
z in cloum a, W(z) in colum b.
Looking for internet famous math prob on dist law.
Click For Summary
Discussion Overview
The discussion revolves around a math problem that gained attention due to its ambiguity and the resulting debate among mathematicians and educators. The problem involves the order of operations in arithmetic expressions, specifically focusing on the expression 6÷2(2+1). Participants reflect on the implications of this problem, its educational value, and related mathematical concepts.
Discussion Character
- Debate/contested
- Conceptual clarification
- Exploratory
Main Points Raised
- Some participants recall a math problem involving order of operations that confused many, including professionals.
- One participant identifies the specific problem as 6÷2(2+1) and questions its difficulty for professional mathematicians.
- Another participant suggests that different calculators yield different answers, although this claim remains untested.
- Some argue that the ambiguity arises from the lack of a formal definition for "implied multiplication," challenging its validity in mathematical literature.
- There are claims that the problem is irrelevant to mathematics and merely a convention that lacks practical significance.
- Participants propose alternative discussion topics, such as the value of 0^0 and whether zero is a natural number, indicating a shift in focus from the original problem.
- Some participants express skepticism about the relevance of the Lambert W function compared to more familiar functions like sine, while others defend its applications in various fields.
- There is a discussion about whether mathematical functions like sine and Lambert W are merely tools or have deeper significance in understanding physical phenomena.
Areas of Agreement / Disagreement
Participants express a range of opinions, with no clear consensus on the significance of the original math problem or the relevance of the Lambert W function. Some view the problem as a valuable teaching tool, while others dismiss it as trivial.
Contextual Notes
The discussion highlights the ambiguity in mathematical notation and the varying interpretations of expressions, which can lead to confusion and disagreement among both students and professionals.
Who May Find This Useful
Mathematics educators, students exploring order of operations, and those interested in the philosophical implications of mathematical functions may find this discussion relevant.
- #32
- 22,170
- 3,327
houlahound said:
Yes, in exactly the same way that one can be computed for the log and the sin function.
- #33
houlahound
- 907
- 223
K, I will give the link a proper read, I stopped when it defined W as inverse branches of something else, what does that even mean.
- #34
- 22,170
- 3,327
It means that the ##W## function is an inverse function.
For example, ##log(z) = w## if and only if ##e^w = z##. This means that the ##\log## is the inverse function of the exponential.
But situations like the log and the exponential aren't always this simple. Take ##w =\sqrt{z}##. It is certainly true that ##w^2 = z##, but ##w## isn't the only value for which ##w^2 = z##, also ##(-w)^2 = z##. So there are two solutions to ##w^2 = z##. We choose one solution (namely the positive one) and call that ##\sqrt{z}##. But we have made a quite arbitrary choice here, we could also take the negative. We say that the square root function has two branches (one for each choice). So there is a negative branch of numbers whose square is ##z## and a positive branch.
In the same way, there is no unique ##w## such that ##we^w = z##. A choice must be made (in some case, in others there is a unique solution). These two choices define two "branches" of the W function.
For example, ##log(z) = w## if and only if ##e^w = z##. This means that the ##\log## is the inverse function of the exponential.
But situations like the log and the exponential aren't always this simple. Take ##w =\sqrt{z}##. It is certainly true that ##w^2 = z##, but ##w## isn't the only value for which ##w^2 = z##, also ##(-w)^2 = z##. So there are two solutions to ##w^2 = z##. We choose one solution (namely the positive one) and call that ##\sqrt{z}##. But we have made a quite arbitrary choice here, we could also take the negative. We say that the square root function has two branches (one for each choice). So there is a negative branch of numbers whose square is ##z## and a positive branch.
In the same way, there is no unique ##w## such that ##we^w = z##. A choice must be made (in some case, in others there is a unique solution). These two choices define two "branches" of the W function.
- #35
houlahound
- 907
- 223
OK this I can do, expansion of W
This also
ETA
This also
ETA
- #36
- 22,170
- 3,327
houlahound said:OK this I can do, expansion of W
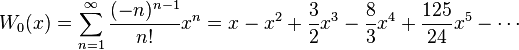
This maybe
Yes, in the same way that the sin and the logarithm have such expansions! You see, there is little difference between the W and the logarithm. The only difference is that you've learned the log at a young age and thus are more "used" to it.
- #37
houlahound
- 907
- 223
But this discussion started that W can not be expressed by more elementary functions when from above clearly it can.
I have really enjoyed and value this discussion cos I got some new math. Appreciate you sticking with.
I have really enjoyed and value this discussion cos I got some new math. Appreciate you sticking with.
- #38
- 22,170
- 3,327
houlahound said:
The term elementary function is a technical term with a very specific meaning. You shouldn't put too much importance at these terms. A function being not-elementary doesn't mean it's hard to compute or anything.
Similar threads
High School
Fractional/decimal powers
- · Replies 10 ·
High School
The Paradox of 1 – 1 + 1 – 1 + 1 – 1 + …
- · Replies 5 ·
- · Replies 15 ·
- · Replies 11 ·
- · Replies 96 ·
- · Replies 4 ·
Challenge
Math Challenge - December 2018
- · Replies 67 ·
- · Replies 83 ·
- · Replies 7 ·
High School
The Drunkard's Walk: A Discussion of the Text
- · Replies 17 ·