Luffing Jib Load, With and Without Sheave Pulley

[Herbid]

Homework Statement

Problem w/ Luffing Jib Load, With and Without Sheave Pulley

Relevant Equations

F = M x a

Now I am working with a DIY Luffing Jib Crane.

Mys subcon said that:
Tension of red rope for hanging a blue box load at the tip of the boom i(A) s as the same as hanging it with pulley and tied to the motor/ground_B (System in a Static Load Condition)..
Blue Rope and Pulley weights are neglected.

I assume by the pic C and D.

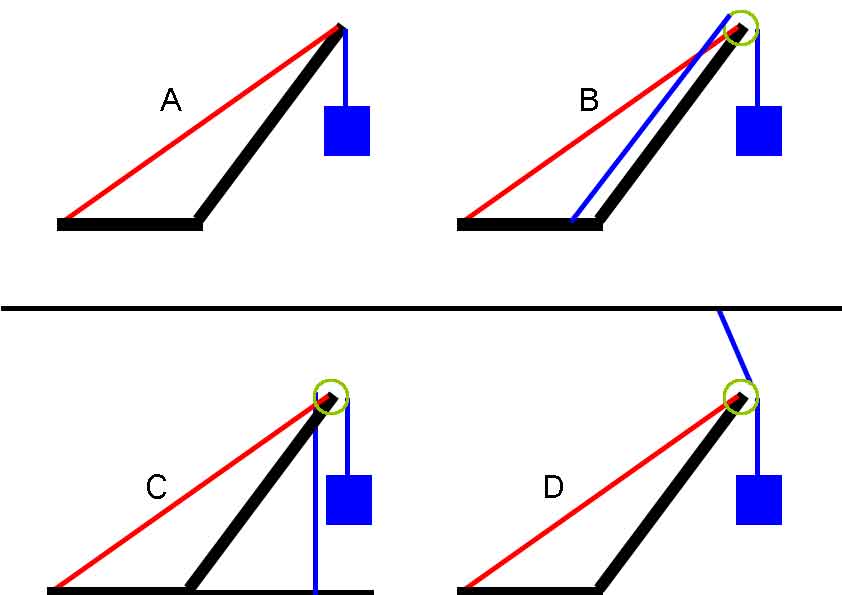
Can anybody give me some advicer?

 

[NascentOxygen]

I assume by the pic C and D.

What are you assuming by (C) and (D)?

Have you established in your mind why there is identical tension in the red cable in (A) and (B)?

 

[gleem]

Other questions you might consider is what is the function of the guy in A? How does it help support the weight. How is its function changed in B?

 

[Herbid]

What are you assuming by (C) and (D)?

Have you established in your mind why there is identical tension in the red cable in (A) and (B)?

It is indeed in C, the tension of red Rope is bigger the in D, because the load in C is double pulled by load and ground.
CMIIW