SUMMARY
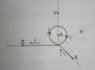
The discussion centers on calculating the magnetic induction B at point A (O, R, O) due to a system of thin conductors carrying current i, specifically a circular conductor of radius R in the yz plane. The magnetic field equations provided are μ₀i/4πr [sinθ₁ + sinθ₂] for a straight wire and μ₀i/2r for a circular arc. Participants emphasize the importance of understanding the contributions to the magnetic field from multiple sources and the necessity of clear communication in problem-solving. The original poster's failure to explain the derivation of four terms from three contributions led to confusion and frustration among helpers.
PREREQUISITES
- Understanding of magnetic fields and induction
- Familiarity with the Biot-Savart Law
- Knowledge of vector components in three-dimensional space
- Proficiency in LaTeX for mathematical expressions
NEXT STEPS
- Study the Biot-Savart Law for magnetic field calculations
- Learn about vector addition and decomposition in physics
- Explore the significance of angles in magnetic field contributions
- Practice deriving magnetic field equations for various conductor configurations
USEFUL FOR
Students studying electromagnetism, physics educators, and anyone involved in solving complex magnetic field problems in theoretical or applied physics.