Homework Help Overview
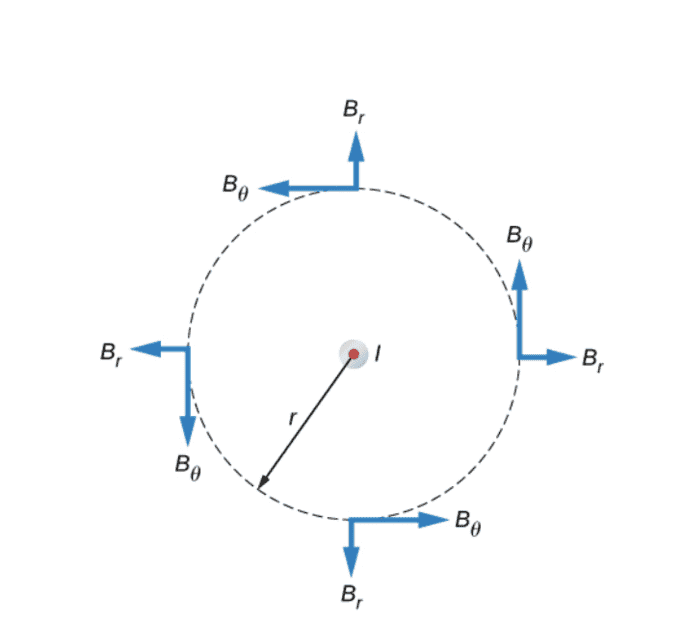
The discussion revolves around understanding the magnetic field generated by an infinitely long current-carrying wire, specifically focusing on the nature of the radial magnetic field and its implications as described by Ampère's law and symmetry arguments.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants explore the concept of a radial magnetic field, questioning how it can exist given the right-hand rule. There are repeated inquiries about the value of the radial component, ##B_r##, and discussions about using symmetry versus Ampère's law to analyze the magnetic field.
Discussion Status
The discussion is active, with participants sharing various perspectives on the use of symmetry and Ampère's law. Some express confusion about how to prove the radial component is zero, while others suggest that symmetry arguments may provide insight. There is no clear consensus, but several participants are engaging deeply with the concepts.
Contextual Notes
Participants note that figures in textbooks may not accurately depict results and that assumptions about the magnetic field's behavior need to be critically examined. There is mention of constraints related to the application of Ampère's law and the nature of vector fields.