formulajoe
- 177
- 0
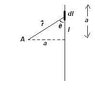
A square conducting loop of side 2a lies in the z=0 plane and carries a current in the counterclockwise direction. Show that at the center of the loop
H = sqrrt2*I/pi*a in the z direction.
I am stuck in this problem. Heres what I've got. I placed the center of the loop at the origin. I am using Biot-Savarts Law. I found an R vector to be sqrt x^2 + y2 in the rho direction and cos x/sqrt x^2 + y2 in the phi direction. Heres where I am stuck. When I go to do the integral, my dl depends on the side I am integrating. So if I am my dl is dx, i don't know how to cross that why R because R has the unit vectors rho and phi.

H = sqrrt2*I/pi*a in the z direction.
I am stuck in this problem. Heres what I've got. I placed the center of the loop at the origin. I am using Biot-Savarts Law. I found an R vector to be sqrt x^2 + y2 in the rho direction and cos x/sqrt x^2 + y2 in the phi direction. Heres where I am stuck. When I go to do the integral, my dl depends on the side I am integrating. So if I am my dl is dx, i don't know how to cross that why R because R has the unit vectors rho and phi.