Magnetic field of a wire within a hollow cylinder.

[freshcoast]

1. Problem statement.

2. Known equations
Amperes law, biot-savart law

3. Attempt.

Just taking steps 1 at a time, I first drew a diagram then I found Jo in terms of I and R, and since it is a non uniform current I know that to find the current I use

J = I / A

substitute A for 2(pi)rdr, and then integrate and solve for Jo,

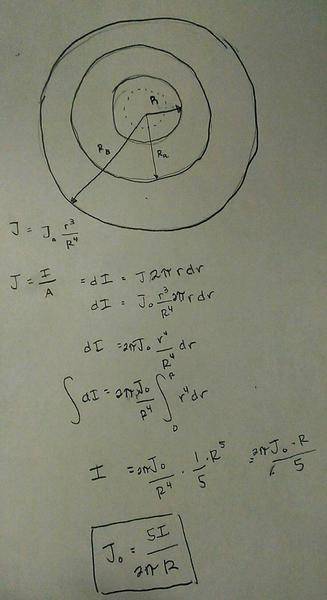
Am I correct as of this far?

 

[TSny]

Looks good to me.

 

[freshcoast]

Awesome!, now this is what I did for the magnetic field inside the wire. Since there is s non uniform current I have to integrate the i.

 

[TSny]

You need a correction in your upper limit of integration. But you are close to setting it up correctly.

(Also, you might want to be more careful in writing your equations. It is not true, for example, that $B (2 \pi r) = \mu_0 J\, 2 \pi r dr$. The right side needs to include the integration in order for the left side to equal the right side.)

 

[freshcoast]

Oh, my upper bound goes to little r. So that changes my value of

B(inside wire) = (mu-knot) * I / 4(pi) *R(wire)

For next question, magnetic field in space between cylinder and wire I believe would be the same as part a.

Part c is a little tricky, since I am working with a non uniform and uniform current, so to tackle this would I just have to first find the current of the whole wire, then the current of the hollow cylinder then just sum them up?

I also had trouble deriving the radius for Ra < r < Rb

 

[TSny]

Oh, my upper bound goes to little r.

Yes, that's right.

So that changes my value of

B(inside wire) = (mu-knot) * I / 4(pi) *R(wire)

No, this can't be right. The magnetic field inside the wire should depend on the distance r from the center of the wire. So, you should recheck your calculation.

For next question, magnetic field in space between cylinder and wire I believe would be the same as part a.

No, the field between the wire and cylinder will have a different dependence on r than the field inside the wire.

Part c is a little tricky, since I am working with a non uniform and uniform current, so to tackle this would I just have to first find the current of the whole wire, then the current of the hollow cylinder then just sum them up?

Yes, you will need to combine the current of the wire with the part of the current in the cylinder that is enclosed by your path of integration. I don't understand your calculation of $I_{wire}$. The current in the wire is given to be $I$ so you don't need to calculate $I_{wire}$. But your expression for the current in the cylinder that is enclosed by your path of integration of radius r looks correct.

I also had trouble deriving the radius for Ra < r < Rb

I'm not sure what you mean here by "deriving the radius".

 

[freshcoast]

Oh I see that I made some arithmetic error for part a)

What I got was

B = (mu-knot * I * (r^4)) / (2pi * (R^5))

Part b)

I am unclear on how to solve this one, if I put a circle just outside of the wire wouldn't the current from the wire still be the same, which is what I found in part a? I think the only thing different will be I am dividing part a by a different r, let's say R(outside) so I have

B = (mu-knot * I * (r^4)) / (2pi * (R^5) * R(outside))

 

[TSny]

Oh I see that I made some arithmetic error for part a)

What I got was

B = (mu-knot * I * (r^4)) / (2pi * (R^5))

Yes, I think that's right.

Part b)

I am unclear on how to solve this one, if I put a circle just outside of the wire wouldn't the current from the wire still be the same, which is what I found in part a?

For part (b), pick any radius r between $R$ and $R_a$. Apply Ampere's law to a circular path of that radius.

 

[freshcoast]

Hmm, I am still unsure, with your suggestion I feel like my answer would still be the same since I am just looking at what is enclosed in my r, which is just the wire alone. But this is the steps I took,

First I need to find the current of the wire, but this time I separated the r that was given and r'. Integrated that to R which is the radius of the whole wire. Then I did some algebraic manipulation to find the current in terms of I and r, and then plugged it in amperes law.

 

[TSny]

In part (a) you are looking for B(r) for some radius r that is less than R. So, you chose an "Amperian" path that is a circle of radius r. You had to find the current inside the path, so you integrated J(r') over the area enclosed by the path of radius r. If r' is the integration variable, then you let r' go from 0 to r.

In part (b) you want B(r) for R < r < Ra. So, now the path is outside the wire. So, think about the current enclosed by this path. You should see that no integration is needed here. (Of course you could integrate over the whole wire if you wanted to, but you already essentially did this in your first post when you were finding an expression for Jo.)

 

[TSny]

In your last post where you set up the integral ∫dI for the whole wire, you should of course get an answer that represents the total current in the wire. This is given to be I, so your integral should reduce to I. The integral should be $\int_0^R J(r')2\pi r'dr'$, but you set it up as $\int_0^R J(r)2\pi r'dr'$ where you used $r$ rather than $r'$ for the argument of $J$.

 

[freshcoast]

Ohh... So for part b since the current is just I and only the wire has that current my magnetic field should just be..

B = (mu-knot * I ) / ( 2*pi*r)

 

[TSny]

Yes. That's it.

 

[freshcoast]

Awesome! Now for part c, using the same logic as before the total current in the wire would just be I, and so I just need to find the distribution of I within the cylinder, which was found above. But this is what I have so far,

 

[TSny]

Your first equation is correct if $I_{cylinder}$ is the part of the current in the cylinder that is enclosed in your dotted path and if $I_{total}$ is the total current in the cylinder. But remember, the total current in the cylinder is given to be $I$ (the same as in the wire).

In your second equation, did you include the current in the wire?

 

[freshcoast]

No I did not, I figured since the radius r is bigger than the wire, the current would've already been included in that I. To account for the current in the wire, do I just add in the current for the whole wire? Which is

Mu-knot * I / 2 * pi * Rwire ??

 

[TSny]

No I did not, I figured since the radius r is bigger than the wire, the current would've already been included in that I. To account for the current in the wire, do I just add in the current for the whole wire? Which is

Mu-knot * I / 2 * pi * Rwire ??

Yes. Whenever you use Ampere's law $\oint \vec{B} \cdot d\vec{s} = \mu_0I_{enclosed}$, the current on the right hand side is the total current passing through the path of integration that you are using on the left side.

 

[freshcoast]

So my final answer for part C, since I am adding in the current of the wire my equation would be

 

[TSny]

Not quite. The very last term inside the brackets on the right is incorrect. Note how the first term in the brackets is dimensionless but the second term is not.

Backing up to $B 2\pi r = \mu_0 I_{enclosed}$, how would you express $I_{enclosed}$?

 

[TSny]

To account for the current in the wire, do I just add in the current for the whole wire? Which is

Mu-knot * I / 2 * pi * Rwire ??

This expression is not the current due to the whole wire. Note that this expression does not have the correct dimensions for a current. It has the dimensions of a magnetic field.

The current in the whole wire is given in the problem to be $I$.

 

[freshcoast]

hmm.. Instead of 1/2 * pi * wire, would it just be 2 * pi * wire?

so

I enclosed = [(r^2) - (Ra^2) / (Rb^2) - (Ra^2)] + [2*pi*wire] ?

what do you mean by dimensionless?

 

[TSny]

$I_{\rm enclosed} = I_{\rm cylinder} + I_{\rm whole wire}$. As stated in the problem, $I_{\rm whole wire} = I$.

"Dimensionless" means that it is a pure number (all the units cancel out).

 

[freshcoast]

Oh..

So

I enclosed = I * [(r^2) - (Ra^2) / (Rb^2) - (Ra^2)] + 1

then

making my equation

B = Mu(knot) * I[enclosed] which was found above?

 

[TSny]

The +1 should be inside the bracket so that $I$ multiplies the +1.

Your expression for B is missing $2\pi r$.

 

[freshcoast]

ah perfect, thank you.

part D, for the field outside the hollow cylinder would then just be

B = mu(knot) * Itotal / 2*pi*r correct?

now for the graphs of each..

for part a ) the graph looks like it would be similar to an r^4 graph
b ) similar to an 1/r graph
c ) I am thinking this one would just be a r^2 / r or r? linear?
d ) would just also look like part b?

 

[freshcoast]

Disregard that, it was not very well thought out. I believe magnetic field outside would be

B = mu knot * [I cylinder + I wire] / 2*pi*r

Since

I cylinder = I

and

I wire = I

I would get

B = mu knot * [I + I] / 2*pi*r

B = mu knot * I * [1 + 1] / 2*pi*r

So

B = mu knot * 2I / 2*pi*r,

And I gave some more thought on my graphs and I believe they will look like this

 

[TSny]

I agree with your result for B outside the cylinder.

Your graph doesn't look correct. Inside the wire, B is proportional to r⁴. So, B should increase in this region.

It looks like your graph is showing B = 0 between the wire and the cylinder and also for outside the cylinder. But you know that isn't right.

 

[freshcoast]

so for part A, the graph should just look like an increasing function, something that looks similar to an $r^4$ graph?

and part b/c/d they just look like a decreasing exponential graph?

 

[TSny]

In the region between the wire and the cylinder and also in the region outside the cylinder (r>Rb) the field will just graph as a constant times 1/r (with different constants for the two regions). Inside the cylinder, B varies as A*r + C/r where A and C are constants.

To get the shape of the graph, you could let $\frac{\mu_0I}{2\pi} = 1$ and choose, say, $R_{\rm wire} = 1$, $R_a = 3$ and $R_b = 5$. Then plot some points in each region.