Magnetic flux given magnetic field and sides (using variables)

[cestlavie]

Homework Statement

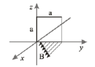
A square loop of sides "a" lies in the yz plane with one corner at the origin. A varying magnetic field B = ky. points in the positive x direction and passes through the loop (k is a constant). The magnetic flux through the loop is: $ka^3/2$ or $ka^3/3$ or $ka^2/2$ or $ka^2$ or none of the above.

Relevant Equations

$Magnetic~flux=ABcos\theta$
$B=k_y$
$A= a^2$

I know the answer is $ka^3/2$. I got $ka^2$ and I don't know how to get the right answer. I saw an explanation using integrals, but my class is algebra-based. My attempt:
$Flux=ABcos\theta$. I figure $cos\theta$ is 1 because the angle between the magnetic field and the normal to the plane is 0.
$Flux=AB$
$Flux=ka^2$
Please point me in the right direction. Thank you!

 

[TSny]

$Flux=AB$
$Flux=ka^2$

In going from the first equation to the second equation, what did you use for $A$ and what did you use for $B$?

 

[cestlavie]

In going from the first equation to the second equation, what did you use for $A$ and what did you use for $B$?

@TSny I used $a^2$ for A and $k$ for B. B is technically $k_y$ but the answer options do not include the subscript.

 

[TSny]

@TSny I used $a^2$ for A and $k$ for B. B is technically $k_y$ but the answer options do not include the subscript.

I don't think $y$ is a subscript. The magnetic field varies with position as $B = ky$. At the left side of the square where $y = 0$, you have $B = 0$. At the right side where $y = a$, you have $B = ka$.

 

[cestlavie]

I don't think $y$ is a subscript. The magnetic field varies with position as $B = ky$. At the left side of the square where $y = 0$, you have $B = 0$. At the right side where $y = a$, you have $B = ka$.

@TSny My professor formatted y as a subscript -_-. That explains the cubed value, but I still don't see where 0.5 comes from. If $B=ky$ and $A=a^2$:
$Flux = BA = (ka)(a^2) = ka^3$

 

[TSny]

@TSny
$Flux = BA = (ka)(a^2) = ka^3$

Here you substituted $B = ka$. But that's the value of $B$ at the far right edge of the square. For most of the square, the B-field is not that strong. You'll need to think about an appropriate average value of B to use.

 

[cestlavie]

Here you substituted $B = ka$. But that's the value of $B$ at the far right edge of the square. For most of the square, the B-field is not that strong. You'll need to think about an appropriate average value of B to use.

@TSny Got it. So they used $B=\frac {k^a} {2}$ for the average value, resulting in the answer with 0.5.

 

[TSny]

@TSny Got it. So they used $B=\frac {k^a} {2}$ for the average value, resulting in the answer with 0.5.

Yes. Nice work.