toneboy1
- 172
- 0
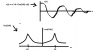
Hi All, I'm just trying to practice graphing signals in frequency domain and I came across a stiuation I wasn't familiar with. If the exp() has a constant*t in it I'm not sure how to graph it, I remember that just cos it like a double sided exp(jwt) but with half the magnitude. I've attached a drawing to better illustrate the question of how to graph X(w),
I've worked out that X(w) = 1/2[1/(3+j(w-10)) + 1/(3+j(w+10))] from x(t) but not sure what that magnitude in frequency domain looks like.
Thanks heaps!
I've worked out that X(w) = 1/2[1/(3+j(w-10)) + 1/(3+j(w+10))] from x(t) but not sure what that magnitude in frequency domain looks like.
Thanks heaps!
Attachments
Last edited: