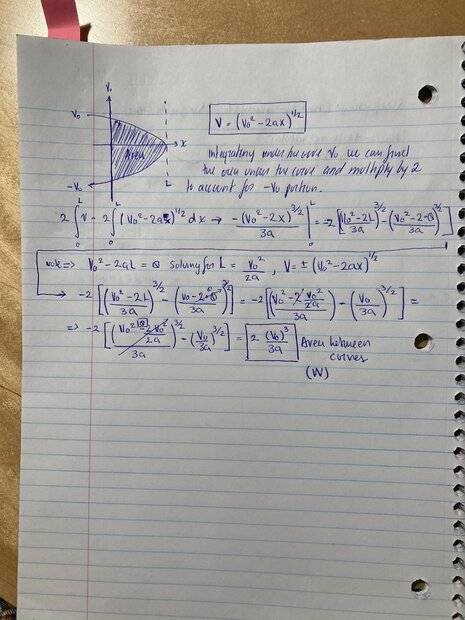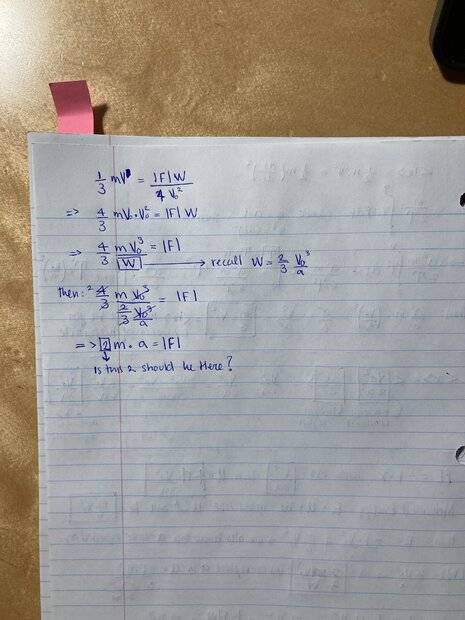SUMMARY
The discussion focuses on deriving the second Newton's law from Mapertius's Principle in the context of perfectly elastic collisions and free fall acceleration. The user reports consistently obtaining a coefficient of 2 in their final calculations, indicating a potential misunderstanding or misapplication of the principles involved. The conversation aims to clarify the derivation process and identify the source of the discrepancy in the calculations.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with Mapertius's Principle
- Knowledge of perfectly elastic collisions
- Basic concepts of free fall acceleration
NEXT STEPS
- Review the derivation of Newton's second law using Mapertius's Principle
- Study the mechanics of perfectly elastic collisions in detail
- Examine examples of free fall acceleration and its mathematical implications
- Explore common pitfalls in physics calculations related to coefficients
USEFUL FOR
Physics students, educators, and anyone interested in the application of classical mechanics principles, particularly in the context of collisions and motion analysis.