Work - Energy Principle Application to Fluid Flow

[Dario56]

In classical and continuum mechanics if we want to find equation of motion of the body we draw force diagram and apply Newton's 2nd law.

In continuum mechanics, equation of motion actually refers to a special point of the body known as center of mass (COM) which can be proven by definition of COM and Newton's 3rd law. Consequence of this proof is that we can pretend like all forces on the body act in COM and that mass of the object is concentrated in it. This is very important proof in continuum mechanics because however complex our body might be, we don't need to care about it as long as we know where is COM and how it moves. To extend on this idea we can apply work - energy principle which states that work done by resultant force equals change in kinetic energy of the COM between two points.

Let us consider fluid flowing in a pipe like in the scheme. We will consider specific derivation of Bernoulli's equation for incompressible fluids given on wikipedia: https://en.wikipedia.org/wiki/Bernoulli's_principle#Derivations_of_the_Bernoulli_equation.

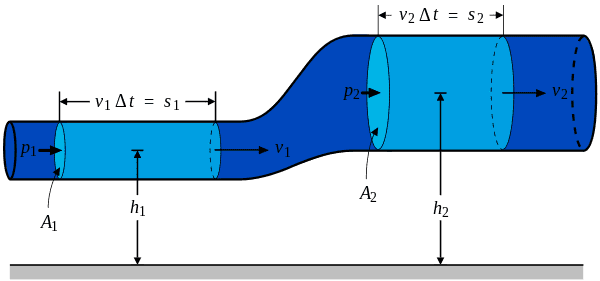
There are 2 types of derivations on wikipedia page, first uses Newton's 2nd law and the other uses conservation of energy or work - energy principle. I am referring to one which uses work - energy principle, section: Derivation by using conservation of energy.

In this derivation, system is defined as fluid volume between two cross sections $A_1$ and $A_2$, respectively . Forces that act on it should cause its center of mass to accelerate, it is just applying Newton's second law or work - energy principle which are basically the same. In our example these forces are only pressure forces and gravity since fluid is inviscid. We will simplify things further by ignoring gravity and pretending like pipe is horizontal so that work done by gravity is zero.

Problem of this derivation is that applying work - energy principle in the way like it is done in this derivation, can only compute changes in kinetic energy of CENTER of MASS of fluid volume which is initially placed between two cross sections, NOT how kinetic energy of fluid changes between two cross sections. We want to know how does pressure difference on two cross sections cause fluid to accelerate between them. We want to watch fluid as it starts moving from one cross section to another. We can do that only if we define differential volume element on cross section 1 and do line integral of pressure gradient along streamline until we get to cross section 2.

Since in this derivation, fluid volume element on which force diagram and work - energy principle is applied is not of differential size, it is not useful since nobody cares in fluid mechanics how much does kinetic energy of COM of fluid volume element change as it flows, but how much does kinetic energy change as fluid flows from point to point.

 

[Chestermiller]

Since you are a Chemical Engineer, you must be familiar with the derivations on the equations in Transport Phenomena by Bird, Stewart, and Lightfoot, both from the macroscopic (control volume) standpoint and from the differential force balance standpoint. And, in the book, they demonstrate mathematically the transition from one to the other. So, specifically, what part of their derivations are you doubtful about?

 

[Dale]

Problem of this derivation is that applying work - energy principle in the way like it is done in this derivation, can only compute changes in kinetic energy of CENTER of MASS of fluid volume which is initially placed between two cross sections, NOT how kinetic energy of fluid changes between two cross sections.

It sounds like you are objecting specifically to the step where they say

The increase in kinetic energy is $$\Delta E_{\text{kin}}={\tfrac {1}{2}}\Delta m\,v_{2}^{2}-{\tfrac {1}{2}}\Delta m\,v_{1}^{2}$$

If so, then I agree. This does not seem to be correctly written. At least, it is a correct expression, but it does not follow directly from the work energy theorem. Since they have claimed to be using the work energy theorem they need to show how to get to this expression from that.

 

[Dario56]

Since you are a Chemical Engineer, you must be familiar with the derivations on the equations in Transport Phenomena by Bird, Stewart, and Lightfoot, both from the macroscopic (control volume) standpoint and from the differential force balance standpoint. And, in the book, they demonstrate mathematically the transition from one to the other. So, specifically, what part of their derivations are you doubtful about?

As far as I know, in that textbook, control volume is used to derive it which is a different approach than one used here. I don't know about the other approaches in that textbook. However, we are now probably going away from my original question/concern given in the main text.

 

[Dario56]

It sounds like you are objecting specifically to the step where they say
If so, then I agree. This does not seem to be correctly written. At least, it is a correct expression, but it does not follow directly from the work energy theorem. Since they have claimed to be using the work energy theorem they need to show how to get to this expression from that.

Well, not really specifically to that.

If we defined our system as fluid volume between two cross sections, pressure force difference should cause acceleration of COM of our system. Acceleration we calculate from Newton's 2nd law is the acceleration of COM. But, who cares about COM. We want to know how fluid changes velocity between two cross sections, not have its COM moves or what are its changes in kinetic energy.

I think no one really understands what I am asking. It is funny .

 

[Dale]

Well, not really specifically to that.

Then please QUOTE specifically what you are objecting to. I mean a direct word for word quote of the problematic part.

I think no one really understands what I am asking. It is funny

I don't think it is very funny, and if it gets shut down again there will not be an opportunity to reopen it. Your next post needs to have the direct quote you find objectionable.

 

[Arjan82]

If we defined our system as fluid volume between two cross sections, pressure force difference should cause acceleration of COM of our system. Acceleration we calculate from Newton's 2nd law is the acceleration of COM. But, who cares about COM. We want to know how fluid changes velocity between two cross sections, not have its COM moves or what are its changes in kinetic energy.

It is perfectly valid to talk about a body of water in a control volume, the forces acting on it and its COM, as long as there is no flow over the boundaries of the control volume. I don't see why you object to that. So, who cares about the COM? I do... I don't see why you wouldn't.

However, the control volume approach cannot give you any information about local velocities. Only about the state of that control volume. So if you want more detailed information, you need to take a different approach. This however does not invalidate the COM approach...

The analysis of the pipe as you show it does draw the control volumes at two very specific locations: where there is no change in height and diameter anymore. So at that location the flow is uniform again (at least, according to the inviscid model). This means that the velocity of the COM is equal to the velocity in the entire volume at that location.

 

[Chestermiller]

Since, in your situation, the system is operating at steady state, the change in kinetic energy from this equation is the same as that experienced by the fluid elements (masses) passing through the control volume from entrance to exit (summed over the control volume).

 

[Dario56]

Then please QUOTE specifically what you are objecting to. I mean a direct word for word quote of the problematic part.

I don't think it is very funny, and if it gets shut down again there will not be an opportunity to reopen it. Your next post needs to have the direct quote you find objectionable.

I've written objection few times already. In my main post, once again to your reply and also in deleted post. I also made a little joke to make discussion more relaxed, but it doesn't mean I am not serious about the discussion.

I've written three long posts about the question and discussed with many people in comments, so that we are clear.

So, to repeat my question once again. Here it comes in the next sentence.

Then please QUOTE specifically what you are objecting to. I mean a direct word for word quote of the problematic part.

I don't think it is very funny, and if it gets shut down again there will not be an opportunity to reopen it. Your next post needs to have the direct quote you find objectionable.

I made a joke to make discussion more relaxed, but that doesn't mean I am not here for serious discussion. After all, I've written three long posts and discussed with everyone in comments normally, so that we are clear about my intentions.

Quote from wikipedia: "the change in the kinetic energy Ekin of the system equals the net work W done on the system."

Since we defined SYSTEM as being initially between two cross sections and because there are unbalanced forces acting on it, it must accelerate due to Newton's 2nd law. System moves in direction of the resultant force, it must if unbalanced forces act on it. So, if pressure forces act on system while it moves or flows, work is done by these forces which must increase its kinetic energy of its COM. But, let me ask you a question. When did you hear anyone talking about center of mass in fluid mechanics? I never did. And that brings us to the objection. By using this derivation, you can only calculate kinetic energy change of COM, NOT how velocity of fluid changes between cross sections $A_1$ and $A_2$. Do you understand what I am asking?

 

[Dario56]

It is perfectly valid to talk about a body of water in a control volume, the forces acting on it and its COM, as long as there is no flow over the boundaries of the control volume. I don't see why you object to that. So, who cares about the COM? I do... I don't see why you wouldn't.

However, the control volume approach cannot give you any information about local velocities. Only about the state of that control volume. So if you want more detailed information, you need to take a different approach. This however does not invalidate the COM approach...

The analysis of the pipe as you show it does draw the control volumes at two very specific locations: where there is no change in height and diameter anymore. So at that location the flow is uniform again (at least, according to the inviscid model). This means that the velocity of the COM is equal to the velocity in the entire volume at that location.

When I say that no one cares about it I mean no one is interested to find how does COM of our fluid volume initially between cross sections move in space in time. We are interested in how does fluid velocity change from point to point - from cross section $A_1$ to $A_2$ and you can't find that out using this derivation because it only allows you to track how COM of the fluid volume moves in space and time.

Since this is derivation of Bernoulli's equation and Bernoulli's equation allows us to track how fluid velocity changes from point to point. But, as I said, this derivation doesn't allow us to track what Bernoulli's equation does since no one ever mentions COM of fluid volume element when using it.

 

[Dale]

Quote from wikipedia: "the change in the kinetic energy Ekin of the system equals the net work W done on the system."

That specific quote is valid. It is just a statement of the work energy principle, which is valid and applies to this system.

Since we defined SYSTEM as being initially between two cross sections and because there are unbalanced forces acting on it, it must accelerate due to Newton's 2nd law. System moves in direction of the resultant force, it must if unbalanced forces act on it. So, if pressure forces act on system while it moves or flows, work is done by these forces which must increase its kinetic energy of its COM.

Yes, which is why the quoted sentence is indeed valid.

But, let me ask you a question. When did you hear anyone talking about center of mass in fluid mechanics? I never did. And that brings us to the objection. By using this derivation, you can only calculate kinetic energy change of COM, NOT how velocity of fluid changes between cross sections A1 and A2.

Sure, but you can derive how the velocity of the fluid changes by calculating the change in KE of the COM. That is the point of the derivation. You don't need to start with the velocity field as long as you end with it. It is perfectly acceptable to use the COM in the middle.

Unfortunately for this derivation, the part that I quoted above is asserted without deriving the connection between the COM and the velocity field. But there is nothing wrong with using the COM to derive the velocity field.

 

[Dario56]

That specific quote is valid. It is just a statement of the work energy principle, which is valid and applies to this system.

Yes, which is why the quoted sentence is indeed valid.

Sure, but you can derive how the velocity of the fluid changes by calculating the change in KE of the COM. That is the point of the derivation. You don't need to start with the velocity field as long as you end with it. It is perfectly acceptable to use the COM in the middle.

Unfortunately for this derivation, the part that I quoted above is asserted without deriving the connection between the COM and the velocity field. But there is nothing wrong with using the COM to derive the velocity field.

Yes, but if we defined our system as moving fluid volume initially between cross sections $A_1$ and $A_2$ than its COM is not initially at cross section $A_1$ and the goal of Bernoulli's equation is to be able to connect changes in velocity on cross sections with pressure differences on them. Since COM is not initially at cross section $A_1$, I can't say what velocity fluid has there and so it breakes the point of Bernoulli's equation.

 

[Chestermiller]

Yes, but if we defined our system as moving fluid volume initially between cross sections $A_1$ and $A_2$ than its COM is not initially at cross section $A_1$ and the goal of Bernoulli's equation is to be able to connect changes in velocity on cross sections with pressure differences on them. Since COM is not initially at cross section $A_1$, I can't say what velocity fluid has there and so it breakes the point of Bernoulli's equation.

Do you want me to derive the equation along a streamline starting from the differential force balance? It leads to the same result as the control volume development.

 

[Dario56]

Do you want me to derive the equation along a streamline starting from the differential force balance? It leads to the same result as the control volume development.

Thank you for the help, however this isn't neccesary because I do agree with that derivation while this one (which is commonly used) is not clear to me and I want to solve my vagueness with this type of derivation.

 

[Dale]

Yes, but if we defined our system as moving fluid volume initially between cross sections $A_1$ and $A_2$ than its COM is not initially at cross section $A_1$ and the goal of Bernoulli's equation is to be able to connect changes in velocity on cross sections with pressure differences on them. Since COM is not initially at cross section $A_1$, I can't say what velocity fluid has there and so it breakes the point of Bernoulli's equation.

Agreed. That is what needs to be fixed. Not the use of the work energy theorem, but the connection between that and the velocity field. There is nothing wrong with using the COM to derive the velocity field, but that should be explicit.

 

[vanhees71]

The mathematical tool to derive balance equations from the hydrodynamical equations are Reynold's transport theorems (of course the name origins from this specific application of them). For volume integrals it reads
$$\mathrm{d}_t \int_{V(t)} \mathrm{d}^3 x f(t,\vec{x})=\int_{V(t)} \mathrm{d}^3 x \partial_t f(t,\vec{x}) + \int_{\partial V(t)} \mathrm{d}^2 \vec{a} \cdot \vec{v}(t,\vec{x}) f(t,\vec{x}).$$
Here $V(t)$ is an arbitrary time-dependent volume and $\partial V(t)$ its boundary. The surface-normal vectors along this boundary are pointing outwards by definition, as usual in 3D vector analysis, $\vec{v}(t,\vec{x})$ is the velocity of the volume element at position $\vec{x}$.

For fluid mechanics $V(t)$ is the volume containing specific physical fluid elements, and $\vec{v}$ is thus the usual velocity (flow) field describing the fluid (in Eulerian description). You can then express the mass conservation law for this material portion of the fluid in integral form simply as
$$\mathrm{d}_t \int_{V(t)} \mathrm{d}^3 x \rho(t,x)=\int_{V(t)} \mathrm{d}^3 x \partial_t \rho(t,\vec{x}) + \int_{\partial V(t)} \mathrm{d}^2 \vec{a} \cdot \rho(t,\vec{x}) \vec{v}(t, \vec{x})=0.$$
Using Gauß's Theorem you can write this as
$$\int_{V(t)} \mathrm{d}^3 x [\partial_t \rho + \vec{\nabla} \cdot (\rho \vec{v})]=0.$$
Since this holds for any material volume you can make it arbitrarily small, from which you get the local form of the conservation law,
$$\partial_t \rho + \vec{\nabla} \cdot \vec{j}=0, \quad \vec{j}=\rho \vec{v}.$$
Now consider momentum, assuming we have some external "volume force" (like a gravitational or electromagnetic field). Then Newton's Law reads
$$\mathrm{d}_t \int_{V(t)} \mathrm{d}^3 x \rho v_j = \int_{V(t)} \mathrm{d}^3 x \partial_t (\rho v_j) + \int_{\partial V(t)} \mathrm{d}^2 a_k \rho v_j v_k=\int_{V(t)} \mathrm{d}^3 x [\partial_t (\rho v_j) + \partial_k (\rho v_j v_k)]=\int_{V(t)} \mathrm{d}^3 x f_j-\int_{\partial V(t)} \mathrm{d} a_j P.$$
Here $P$ is the pressure (assuming an ideal fluid). The surface integral on the right-hand side is the force on the fluid volume due to the pressure from the fluid around this volume. Further using Gauß's integral theorem again, you have
$$\int_{\partial V(t)} \mathrm{d} a_j P =\int_{V(t)} \mathrm{d}^3 x \partial_j P.$$
Then you can write everything on both sides in a volume integral, leading to
$$\partial_t (\rho v_j) + \partial_k (\rho v_j v_k)=f_j - \partial_j P.$$
Using the mass-conservation continuity equation from above this leads to the Euler equation for the perfect fluid, as it must be
$$\rho (\partial_t v_j + v_k \partial_k v_j=f_j-\partial_j P,$$
or in vector notation
$$\rho (\partial_t \vec{v} +(\vec{v} \cdot \vec{\nabla}) \vec{v}=\vec{f}-\vec{\nabla} P.$$
Finally we can write down the energy balance equation. Let $u$ be the internal energy per unit mass of the fluid. Then
$$E=\int_{V(t)} \mathrm{d}^3 x \left [\frac{\rho}{2} \vec{v}^2 + \rho u \right].$$
The energy balance reads
$$\mathrm{d}_t E=\int_{V(t)} \mathrm{d}^3 x \vec{f} \cdot \vec{v} - \int_{\partial V} \mathrm{d} \vec{a} \cdot \vec{v} P = \int_{V(t)} \mathrm{d}^3 x [\vec{f} \cdot \vec{v}-\mathrm{\nabla} \cdot (\vec{v} P)].$$
The left-hand side can be transformed with Reynold's transport theorem to
$$\mathrm{d}_t E=\int_{V(t)} \mathrm{d}^3 x \left \{ \partial_t \left [ \frac{\rho}{2} \vec{v}^2 + \rho u \right] + \vec{\nabla} \cdot \left [ \vec{v} \left ( \frac{\rho}{2} \vec{v}^2 + \rho u \right) \right ] \right \}.$$
Using both expressions for $\mathrm{d}_t E$, bringing the divergence terms to one side of the equation and using
$$\rho u+P=\rho(u+P/\rho)=\rho h,$$
where $h$ is the enthalpy per unit mass of the fluid, we finally get the energy-balance equation
$$\partial_t \left [ \frac{\rho}{2} \vec{v}^2 + \rho u \right] + \vec{\nabla} \cdot \left [\vec{v} \left (\frac{\rho}{2} \vec{v}^2 + \rho h \right) \right]=\vec{f} \cdot \vec{v},$$
where we have used again that the above consideration holds for any material fluid volume $V(t)$. As the derivation shows, that's nothing else than the continuum-mechanical version of the work-energy theorem of Newtonian mechanics.

 

[Arjan82]

But, let me ask you a question. When did you hear anyone talking about center of mass in fluid mechanics? I never did. And that brings us to the objection.

This is not an argument. The fact that you or anyone else never heard of it, doesn't make it wrong. If you want us to help you, you need to specify what exactly you think is wrong with the COM analysis, because once again: it is perfectly valid...

By using this derivation, you can only calculate kinetic energy change of COM, NOT how velocity of fluid changes between cross sections $A_1$ and $A_2$. Do you understand what I am asking?

That can easily be solved: if you are interested in how the velocity changes between A1 and A2, then just make sure the COM is intersecting with these planes. Then, when reading your own arguments, you should agree with me that you do know how the velocity changes between A1 and A2 since indeed you know the velocity change of the COM.

However, that is actually not necessary. The start and end control volumes that are drawn are cylinders. If the flow is homogeneous through one plane (you do need to make that assumption) then the velocity in the entire cylinder is equal to the velocity of the COM as I stated earlier...

Since COM is not initially at cross section $A_1$,

So, then choose a control volume that does have the COM at A1...

 

[Arjan82]

By the way, you insist that the given analysis needs to give the fluid velocities. Well, Bernoulli is not going to be sued if his equations do not give that. Strictly speaking the analysis only tells you something about the velocity of the control volume (or even more so, of its COM). Not of the local velocities, it doesn't say that anywhere. If that's not good enough for you, then you need to perform a different kind of analysis, but you should not blame Bernoulli for not giving you the answer you want. It also does not invalidate the Bernoulli approach.

But, once more, because the cylindrical shape of the control volumes at the start and finish of the two control volumes, the velocity of the COM has to be equal to the local velocity of the fluid.

This is not always true, if the control volume is moving through a corner, then the COM velocity is not directly related to the local velocity (I think indeed it differs).

[edit] by 'the Bernoulli approach' I mean the control volume approach. Because as stated a few times, you can derive the Bernoulli equation for a fluid parcel along a streamline, in which case you can say more about the local velocities.[/edit]

 

[Dario56]

This is not an argument. The fact that you or anyone else never heard of it, doesn't make it wrong. If you want us to help you, you need to specify what exactly you think is wrong with the COM analysis, because once again: it is perfectly valid...
That can easily be solved: if you are interested in how the velocity changes between A1 and A2, then just make sure the COM is intersecting with these planes. Then, when reading your own arguments, you should agree with me that you do know how the velocity changes between A1 and A2 since indeed you know the velocity change of the COM.

However, that is actually not necessary. The start and end control volumes that are drawn are cylinders. If the flow is homogeneous through one plane (you do need to make that assumption) then the velocity in the entire cylinder is equal to the velocity of the COM as I stated earlier...
So, then choose a control volume that does have the COM at A1...

Thanks for the answer. To reply to your last comment on deleted thread, saying Cauchy equation is really nitpicking .

While derivation on wikipedia should say how COM moves in time and space, it doesn't. That is the problem. It somehow connects pressure difference with change in velocity on two cross sections, while we agreed that this analysis should actually refer to how COM moves not how velocity of fluid changes between cross sections. To be clear, since in this derivation, system is defined as being a fluid volume INITIALLY between two cross sections, forces that act on it should cause its COM to accelerate according to Newton's 2nd law. This fluid volume we picked moves and accelerates in the direction of the resultant force. Here we aren't using control volume approach where control volume is fixed in space and time.

Also, if you say that to obtain how velocity changes between these two cross section, I need to pick a different fluid volume element, you are basically stating that this derivation is invalid in so much that in this derivation that different fluid volume element isn't picked. If we do choose to pick different fluid element so that COM lies on $A_1$, than pressure will not be pressure on cross sections A1 and A2. And so we can't use this derivation to connect pressures with velocities on cross sections like Bernoulli's equation allows us.

I am not saying Bernoulli is wrong. I do agree with him. There are in my opinion better derivations than this one, but I wanted to discuss to see what is a problem with this one since it is often used. I am claiming that this derivation is either wrong or that at most can't provide what we want and because of which it isn't useful.

 

[Arjan82]

The velocity of the COM has to be the average velocity of the fluid in the volume. In the analysis nothing is assumed about the size of x1 and x2. So you can make them arbitrarily small, in which case the velocity of the fluid can get arbitrarily close to the velocity of the COM.

 

[Chestermiller]

The derivation that works best for me is that given in sections 7.4 and 7.8 of Transport Phenomena. This is very rigorous, and includes even viscous fluids.

 

[Dario56]

The derivation that works best for me is that given in sections 7.4 and 7.8 of Transport Phenomena. This is very rigorous, and includes even viscous fluids.

Yes, what you've written is a nice derivation. But, this one on wikipedia which I am discussing know is really sloppy and I am not sure if it is correct.

 

[Dario56]

The velocity of the COM has to be the average velocity of the fluid in the volume. In the analysis nothing is assumed about the size of x1 and x2. So you can make them arbitrarily small, in which case the velocity of the fluid can get arbitrarily close to the velocity of the COM.

Few ideas came to me. First off, I think this derivation actually uses Eulerian viewpoint not Lagrangian like we agreed (it isn't stated what viewpoint is used which isn't very rigorous). So, we use control volume fixed in space ane time and watch how fluid flows in and out of it. Control volume is what they called system in this derivation.

Problem in this derivation is that work energy - principle is incorrectly applied because it is stated that kinetic energy of the system changes as consequence of work done by forces on it. This is wrong because Bernoulli's equation is used for stationary flow and so both kinetic and potential energy in the control volume must remain constant. So kinetic energy of system doesn't change, what changes is fluid velocity between cross sections.

This derivation isn't rigorous and is in fact wrong since it states things which are incorrect, but comes to correct solution nevertheless. It is like in logic, false premises can give you correct conclusion if your reasoning isn't logical or rigorous.

 

[Dale]

This derivation isn't rigorous and is in fact wrong since it states things which are incorrect

I wouldn’t say wrong. It doesn’t state incorrect things, it simply does not fully justify the correct things that it does state. It is sloppy, not wrong.

 

[Dario56]

I wouldn’t say wrong. It doesn’t state incorrect things, it simply does not fully justify the correct things that it does state. It is sloppy, not wrong.

Statement that kinetic energy of fluid in control volume (which is called system in this derivation) changes because of work done by forces on it, is wrong if you define system as it is defined here because fluid's kinetic energy in control volume can't change in stationary flow which is a flow described by Bernoulli's equation. What changes is fluid veloxity on cross sections, not kinetic energy of the system. That is indeed sloppy and wrong.

What is strange to me how often this derivation is used, but you will not find it in any serious fluid mechanics textbook.

 

[Dale]

Statement that kinetic energy of fluid in control volume (which is called system in this derivation) changes because of work done by forces on it, is wrong if you define system as it is defined here because fluid's kinetic energy in control volume can't change in stationary flow which is a flow described by Bernoulli's equation. What changes is fluid veloxity on cross sections, not kinetic energy of the system. That is indeed sloppy and wrong.

What is strange to me how often this derivation is used, but you will not find it in any serious fluid mechanics textbook.

You are misunderstanding their definitions. The “system” is not a stationary control volume, it is an element of fluid. It moves and as it moves its KE does indeed change. As it says: “In the time interval Δt fluid elements initially at the inflow cross-section A1 move …”

 

[Chestermiller]

Statement that kinetic energy of fluid in control volume (which is called system in this derivation) changes because of work done by forces on it, is wrong if you define system as it is defined here because fluid's kinetic energy in control volume can't change in stationary flow which is a flow described by Bernoulli's equation. What changes is fluid veloxity on cross sections, not kinetic energy of the system. That is indeed sloppy and wrong.

What is strange to me how often this derivation is used, but you will not find it in any serious fluid mechanics textbook.

I agree with you. At best, it is confusing.

 

[Dario56]

You are misunderstanding their definitions. The “system” is not a stationary control volume, it is an element of fluid. It moves and as it moves its KE does indeed change. As it says: “In the time interval Δt fluid elements initially at the inflow cross-section A1 move …”

I thought that too, but I think this is not the case because the way derivation is carried out is like with control volume approach. Nowhere is it written that this approach is used, but if you are familiar with that type of derivation, you can see that is actually the case.

I figured this out because Chester derived Bernoulli's equation by control volume approach in one of the threads. Derivation by Chester is on this link: https://www.physicsforums.com/threa...om-work-energy-principle.1008140/post-6554344. This derivation can be found in textbook Transport Phenomena by Stewart, Bird and Lightfoot.

 

[vanhees71]

The derivation that works best for me is that given in sections 7.4 and 7.8 of Transport Phenomena. This is very rigorous, and includes even viscous fluids.

Sect. 7.4 and 7.8 of which book/paper?

 

[Chestermiller]

Sect. 7.4 and 7.8 of which book/paper?

Transport Phenomena, by Bird, Stewart, and Lightfoot.

 

[vanhees71]

That's a more general derivation similar to the one I've given above for the special case of ideal fluids. It's a great book!

 

[Dale]

I thought that too, but I think this is not the case because the way derivation is carried out is like with control volume approach. Nowhere is it written that this approach is used, but if you are familiar with that type of derivation, you can see that is actually the case.

I am familiar with control volume type derivations. But, if you are going to reject what a derivation actually explicitly says and replace it with your own version and criticize your own version then if the resulting derivation is wrong you really have only yourself to blame. It is at that point no longer the Wikipedia derivation but your own personal strawman derivation. To criticize a derivation you must not reinterpret what they say, but accept what they actually do say.

Here they explicitly consider a fluid element. This element moves and changes KE. That is legitimate. Then, since the KE of any given location is constant, they can remove the portion of the fluid element which is shared by both the initial and final element and attribute the change in KE of the whole element to a difference in KE between the unshared portions.

Again, the derivation is sloppy because it does not clearly relate the COM of the work energy theorem to the KE of these unshared portions. But it is not a wrong approach.

 

[Dario56]

I am familiar with control volume type derivations. But, if you are going to reject what a derivation actually explicitly says and replace it with your own version and criticize your own version then if the resulting derivation is wrong you really have only yourself to blame. It is at that point no longer the Wikipedia derivation but your own personal strawman derivation. To criticize a derivation you must not reinterpret what they say, but accept what they actually do say.

Here they explicitly consider a fluid element. This element moves and changes KE. That is legitimate. Then, since the KE of any given location is constant, they can remove the portion of the fluid element which is shared by both the initial and final element and attribute the change in KE of the whole element to a difference in KE between the unshared portions.

Again, the derivation is sloppy because it does not clearly relate the COM of the work energy theorem to the KE of these unshared portions. But it is not a wrong approach.

I didn't reinterpret what they said. Problem arises because I disagree that moving fluid element is used, but control volume actually. Nowhere it is stated that fluid volume element moves nor is it tracked in time as it moves, but masses of fluid that enter and exit control volume are in fact tracked which is exactly control volume approach. In derivation it is stated that in time $\Delta t$ masses $\Delta m$ ENTER AND EXIT the system carrying kinetic and potential energy with it. It didn't say that in time $\Delta t$ fluid element moves as a whole and than tracks its COM .In my opinion, bad derivation which shouldn't be tought in this way.

 

[Dale]

I didn't reinterpret what they said. Problem arises because I disagree that moving fluid element is used, but control volume actually. Nowhere it is stated that fluid volume element moves (emphasis added)

They said “The system consists of the volume of fluid, initially between the cross-sections A1 and A2. In the time interval Δt fluid elements initially at the inflow cross-section A1 move over a distance s1 = v1 Δt” (emphasis added)

I am not sure how you can be unclear. They are clearly talking about the motion of the fluid elements. The use of the work energy theorem is legitimate here.

If you wish to criticize a derivation, then do so, criticize it on its own ground. But don’t make your own strawman and criticize that strawman. I don’t like this derivation either, but your specific criticism of it is a strawman fallacy.

 

[Dario56]

They said “The system consists of the volume of fluid, initially between the cross-sections A1 and A2. In the time interval Δt fluid elements initially at the inflow cross-section A1 move over a distance s1 = v1 Δt” (emphasis added)

I am not sure how you can be unclear. They are clearly talking about the motion of the fluid elements. The use of the work energy theorem is legitimate here.

If you wish to criticize a derivation, then do so, criticize it on its own ground. But don’t make your own strawman and criticize that strawman. I don’t like this derivation either, but your specific criticism of it is a strawman fallacy.

Yes, but this a mistake of this derivation. They say first what you quoted, there is a fluid element between cross sections and than procced by deriving equation like there is a control volume. They mixed two approaches because they say one thing and than two the other. We agreed that if you use fluid element approach, you must compute how COM moves which clearly isn't done and derivation progresses with control volume approach even though it didn't start with that.