just_mb
- 3
- 0
Hi all,
I'm trying to solve a problem of finite square well for the ##s## states graphically. The task is to find energy levels and wavefunctions of proton in a spherically symmetric potential, first for deuteron then ##^{48}Ca##. What makes me confused is the mass. For deuteron, the mass used is the reduced mass because it's a two-masses system. Using that, the energy from my calculation is similar to that from literature. But what about the ##^{48}Ca##, what mass should I use? When I use reduced mass of ##m_{proton}(19 \times m_{proton} + 28 \times m_{neutron})/(20 \times m_{proton} + 28 \times m_{neutron})## which I found from a literature, the energies don't match with realistic Skyrme Hartree Fock calculations (figure attached). When I use the total mass ##(20 \times m_{proton} + 28 \times m_{neutron})##, I found 7 ##s## energy levels as oppose to 2, as shown in the figure. Please help me, I have been searching through tons of books and journals with no luck.
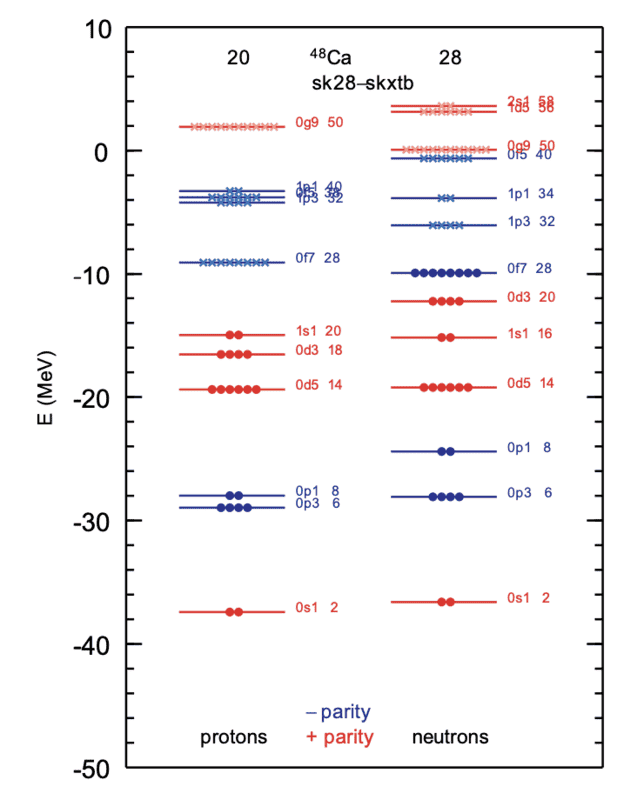
I'm trying to solve a problem of finite square well for the ##s## states graphically. The task is to find energy levels and wavefunctions of proton in a spherically symmetric potential, first for deuteron then ##^{48}Ca##. What makes me confused is the mass. For deuteron, the mass used is the reduced mass because it's a two-masses system. Using that, the energy from my calculation is similar to that from literature. But what about the ##^{48}Ca##, what mass should I use? When I use reduced mass of ##m_{proton}(19 \times m_{proton} + 28 \times m_{neutron})/(20 \times m_{proton} + 28 \times m_{neutron})## which I found from a literature, the energies don't match with realistic Skyrme Hartree Fock calculations (figure attached). When I use the total mass ##(20 \times m_{proton} + 28 \times m_{neutron})##, I found 7 ##s## energy levels as oppose to 2, as shown in the figure. Please help me, I have been searching through tons of books and journals with no luck.
Last edited:
