Mass of Ice required to achieve a certain final Temperature

[CrosisBH]

Homework Statement

An insulated beaker with negligible mass contains a mass of 0.350 kg of water at a temperature of 76.5 °C.
How many kilograms of ice at a temperature of − 23.9 ∘C must be dropped in the water to make the final temperature of the system 40.0 ∘C?
Take the specific heat for water to be 4190 J/(kg⋅K) , the specific heat for ice to be 2100 J/(kg⋅K) , and the heat of fusion for water to be 334 kJ/kg .

Homework Equations

$$Q = mc\Delta T$$
$$Q = mL_f$$

The Attempt at a Solution

I recognized what exactly happened which each part of the system.

Ice at T_ice is heated to 0°C -> Ice is transformed to water -> The water is heated to T_f
Water at T_water is cooled to T_f

So setting up the equation
$$Q_{ice} + Q_{ice\rightarrow water} + Q_{water(ice)} + Q_{water} = 0$$
Expanding
$$m_{ice} c_{ice} (0°C - T_{ice}) + m_{ice}L_f + m_{ice}c_{water}(T_f - 0°C)+m_{water}c_{water}(T_f-T_{water}) = 0$$
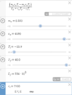
I then solved for m_ice,
$$m_{ice} = \frac{m_{water} c_{water} T_i - m_{water} c_{water} T_f}{L_f + c_{water} T_f - c_{ice} T_{ice}}$$

And then I plugged all the values into Desmos:

L_f was converted from kJ/kg to J/kg. Getting -0.170 kg when doing 3 significant figures. Obviously there's something wrong here. I went through the algebra multiple times, so I think there's something wrong with my Physics.

 

[haruspex]

something wrong with my Physics.

No, just lack of care in notation. Do you notice there's a given number you have not used?

 

[CrosisBH]

No, just lack of care in notation. Do you notice there's a given number you have not used?

Yep. It was bad notation. Dumb me used T_i as both temperature of ice and the initial temperature of water in Desmos. I guess this is a lesson for me to properly name my variables so no confusion can stir from me lol.

 

[scottdave]

Well I find out something new everyday. That Desmos looks impressive. It may be overkill for this type of math problem. Perhaps that is how one of your variables got lost.