Master Vectors: Canoeing to an Island with Help from Our Experts!

[wr1015]

Vectors problem help, please!

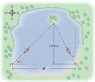
Two canoeists start paddling at the same time and head toward a small island in a lake. Canoeist 1 paddles with a speed of 1.60 m/s at an angle of 45° north of east. Canoeist 2 starts on the opposite shore of the lake, a distance d = 1.59 km due east of canoeist 1.

(a) In what direction relative to north must canoeist 2 paddle to reach the island?? the answer in degrees west of north.
(b) What speed must canoeist 2 have if the two canoes are to arrive at the island at the same time?

 

[LeonhardEuler]

If I understand the problem correctly, there is not enough information. The island could be anywhere in the lake along the line canoeist 1 travels. The direction canoeist 2 travels will depend on exactly where the island is.

 

[wr1015]

If I understand the problem correctly, there is not enough information. The island could be anywhere in the lake along the line canoeist 1 travels. The direction canoeist 2 travels will depend on exactly where the island is.

yes you are quite right, attached is a picture of the problem above

 

[LeonhardEuler]

Look at canoeist 1's path. There is a 45-45-90 triangle consisting of his path, the x-axis, and the perpendicular from the island. Given one of the sides, you can now find the other 2. Now look at canoeist 2's triangle. Since you know the toal distance along the x-axis is 1.59km, and you know one part of it from the 45-45-90 triangle, you can subtract to get the short leg of canoeist 2's triangle. The angle \theta is congruent to the angle in canoeist 2's triangle between the canoeist's path and the long leg, so you know that \tan{\theta}=\frac{opp}{adj}. Solve for \theta

 

[wr1015]

Look at canoeist 1's path. There is a 45-45-90 triangle consisting of his path, the x-axis, and the perpendicular from the island. Given one of the sides, you can now find the other 2.

first i would just like to thank you for actually helping me I greatly appreciate it but for some reason I don't think I fully understand your response because I'm assuming you mean that i use pythagorean's theorem for this but how would that work?? because that would be: (1.59km)squared + unknown side squared = hypotenuse (or the path of canoeist 1) squared.

 

[LeonhardEuler]

first i would just like to thank you for actually helping me I greatly appreciate it but for some reason I don't think I fully understand your response because I'm assuming you mean that i use pythagorean's theorem for this but how would that work?? because that would be: (1.59km)squared + unknown side squared = hypotenuse (or the path of canoeist 1) squared.

It's not the pythagorean theorem you're using. A 45-45-90 triangle is an isocelese triangle. This means that the two legs are of equal length. I am looking at the triangle that has it's sides as: 1-the canoeist 1's path, 2-the side labled 1km, 3-the bottom. The fact that the two legs are equal means that the length of the bottom side is also 1km. The total distance along the bottom between the canoers is 1.59km, so the remaining length must be .59. From there, do what I said before to get the angle. Also, once you have that bottom part for canoeist 1's triangle, you can use the pythagorean theorem to find canoeist 1's path length.

 

[wr1015]

It's not the pythagorean theorem you're using. A 45-45-90 triangle is an isocelese triangle. This means that the two legs are of equal length. I am looking at the triangle that has it's sides as: 1-the canoeist 1's path, 2-the side labled 1km, 3-the bottom. The fact that the two legs are equal means that the length of the bottom side is also 1km. The total distance along the bottom between the canoers is 1.59km, so the remaining length must be .59. From there, do what I said before to get the angle. Also, once you have that bottom part for canoeist 1's triangle, you can use the pythagorean theorem to find canoeist 1's path length.

thank you very much, that helped me greatly