Mastering Derivatives: Tips and Tricks for Calculus Success

[mathzeroh]

In light of my current failure of the first exam of my calculus class, I've been a bit discouraged, but i try not to let these grades get me down.

with that said, can anyone be so kind as to help me wrap my mind around the concept of derivatives? i have a shaky understanding of them as it is, therefore, any help or tips that you all may have, is greatly appreciated. how did you learn about them? what helped you go, "OH! i get it now!" ?

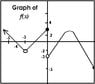
for example, how do i find this:

f'(-4)

and all I'm given is a graph of f(x).

any help on this?? i greatly appreciate it in advance! thank you!

i tried my best to duplicate the graph, though it may be a poor representation. my apologies.

 

[d_leet]

Well think about what a derivative is? What does the derivative of a function at a specific point mean?

 

[mathzeroh]

i know that at a specific point, it's the equation of the tangent line.

but what about that example problem?

 

[HallsofIvy]

i know that at a specific point, it's the equation of the tangent line.

but what about that example problem?

Well, that's your first problem- you know wrong!

The derivative of a function, at a specific point, is the slope of the tangent line to the graph at that point, a number, not the equation of the tangent line.

Now, it isn't easy to sketch the graph of f ' just by eyeballing the graph of f but in your specific case it looks like the graph is largely made of straight lines. Can you find the slope of those? Of course, where the graph is a straight line, the derivative at each point is the slope. Also you should be able to easily see where the derivative is positive, negative, or zero.

Be careful about places where the derivative does not exist.

 

[mathzeroh]

Now, it isn't easy to sketch the graph of f ' just by eyeballing the graph of f but in your specific case it looks like the graph is largely made of straight lines. Can you find the slope of those? Of course, where the graph is a straight line, the derivative at each point is the slope. Also you should be able to easily see where the derivative is positive, negative, or zero.

Be careful about places where the derivative does not exist.

i don't understand. what about the quotient formulas?

 

[d_leet]

i don't understand. what about the quotient formulas?

I don't understand what that has to do with you're initial problem... You aren't differentiating a function you're trying to estimate the derivative at a point.

 

[HallsofIvy]

The derivative at a point is the slope of the tangent line at that point. If the graph happens to be a straight line, then the derivative at each point is the slope of that line.

You asked specifically about f'(-4). From your graph it looks like the graph there is a straight line through (-3, -2) and (-5, 2). What is the slope of that line?

 

[mathzeroh]

the slope of that line is:

2-(-2)/(-5)-(-3)

=2+2/-5+3

=4/-2

=(-2)

is that it?

 

[mathzeroh]

The derivative at a point is the slope of the tangent line at that point. If the graph happens to be a straight line, then the derivative at each point is the slope of that line.

You asked specifically about f'(-4). From your graph it looks like the graph there is a straight line through (-3, -2) and (-5, 2). What is the slope of that line?

so was that it? -2?

 

[HallsofIvy]

so was that it? -2?

Is it what? You were originally asking about f '(-4). One of the first things you should have learned about the derivative at a point is that it is the slope of the tangent line at that point. In particular if a graph is a straight line on an interval, its derivative at any point in that interval is its slope.

 

[VietDao29]

Is it what? You were originally asking about f '(-4). One of the first things you should have learned about the derivative at a point is that it is the slope of the tangent line at that point. In particular if a graph is a straight line on an interval, its derivative at any point in that interval is its slope.

But I thought his post #8, apart from some missing parentheses, is correct...
Isn't it?

 

[mathzeroh]

Is it what? You were originally asking about f '(-4). One of the first things you should have learned about the derivative at a point is that it is the slope of the tangent line at that point. In particular if a graph is a straight line on an interval, its derivative at any point in that interval is its slope.

well thanks a lot for your help. that makes sense. i guess its just something that will take a little while to sink in completely, but i know that once know it fully, i'll be better at knowing what to do. so the answer to my question of f'(-4) in that problem was -2, though right? (just like VietDao said?)