Mathematica: Mapping a Four Color Rectangle to a Four Color Torus

[aheight]

Hi,

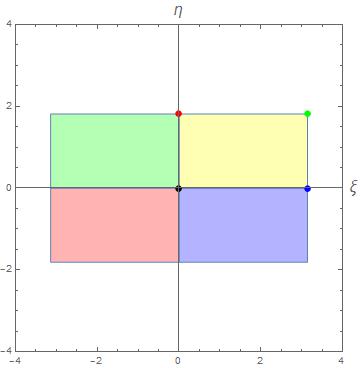
I was wondering if someone could help me understand the grid command in the following Mathematica code that transforms a rectangle to a torus like in this video below. My problem is I want the blue rectangle in the Mathematica code to look like the four color rectangle in the plot below. Basically want to map the four color rectangle to a four color torus. I got the Mathematica code on line and I'm having problems understanding the code to change it to my color map.

DynamicModule[{x = 2., l = 100., x2 = 2., l2 = 100., grid, fast,
  slow}, Grid[{{Graphics3D[{Dynamic[
       Map[{Blue, Polygon[#[[{1, 2, 4, 3}]]]} &,
          Join @@@ (Join @@ Partition[#, {2, 2}, 1])] &[
        ControlActive[fast[l, l2], slow[l, l2]]]]},
     PlotRange -> {{-7, 7}, {-7, 7}, {-1, 2}}, ImageSize -> 600,
     Axes -> True, BaseStyle -> 18],
    Column[{Slider[Dynamic[x, (l = 10.^#; x = #) &], {.0001, 2.}],
      Slider[Dynamic[x2, (l2 = 10.^#; x2 = #) &], {.0001, 2.}]}]}}],
Initialization :> (grid[l_, l2_, n_, m_] :=
    Outer[Compose,
     Array[RotationTransform[# Pi/l2, {0, 0, 1.}, {0, -l2, 0}] &,
      n, {-1, 1}],
     Array[RotationTransform[# Pi/l, {1., 0, 0}, {0, 2, l}][{0, 2,
         0}] &, m, {-1, 1}], 1];
   fast[l_, l2_] = grid[l, l2, 10, 10];
   slow[l_, l2_] = grid[l, l2, 50, 25];)]

.

Thanks for reading.

 

[aheight]

Hi guys,

Here is my solution to the problem:

nMax=10;

etaMax=1.8138
grid[l_,l2_,n_,m_]:=Outer[Compose,Array[RotationTransform[# \[Pi]/l2,{0,1.,0},{0,0,l2+2}]&,n,{-1,1}],Array[RotationTransform[# etaMax/l,{1.,0,0},{0,0,l}][{0,0,0}]&,m,{-1,1}],1]

gVal=Table[Lighter[Green,0.3],{nMax},{nMax}];
rVal=Table[Lighter[Red,0.3],{nMax},{nMax}];
yVal=Table[Lighter[Yellow,0.3],{nMax},{nMax}];
bVal=Table[Lighter[Blue,0.3],{nMax},{nMax}];
mt1=MapThread[{#1,#2}&,{bVal,yVal}];
mt2=MapThread[{#1,#2}&,{rVal,gVal}];
myColors2=Flatten[Join[mt1,mt2]];

Manipulate[Show[{Graphics3D[MapThread[{#1,Polygon[#2[[{1,2,4,3}]]]}&,{myColors2,Join@@@(Join@@Partition[grid[10.^val1,10.^val2,2 nMax+1,2 nMax+1],{2,2},1])}]]},PlotRange->{{-6,6},{-6,6},{-6,6}},Axes->True,AxesLabel->{Style["X",16],Style["Y",16],Style["Z",16]}],{val1,\[Pi],-.235 },{val2,\[Pi],0.0001}]