Mathematical Representation of a Traveling Wave

[Violagirl]

Homework Statement

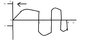
A wave is represented by y = A sin (kx + ωt). Draw two cycles of the wave from x = 0 to x = 2λ at a) t = 0; b) t = T/4, where T = 1/f = 2∏/ω

Homework Equations

y = A sin (kx+ωt)

k = 2∏/λ (number of wave peaks)

The Attempt at a Solution

I had a really hard time on this problem. From what I could do, for part a, I plugged in t = 0 and from that, I know we would end up with the equation:

y = A sin (kx)

From this, I gathered that the wave would be traveling in a -x direction since the sin function is positive. Outside of that though, I had no idea or understanding how to properly draw it...

Part b, the best I could gather is that in plugging in t = T/4, we'd get an equation of:

y = A sin (kx +ω(T/4)).

In taking T = 2∏/ω

We can find ω and get an equation of:

ω = 2∏/T

So our equation will then look like:

y = A sin (kx + (2∏/T) (T/4))

In simplifying the equation further, we get:

y = A sin (kx +∏/2)

Once again though, I'm lost how to properly draw it. I would really appreciate any guidance on to go about drawing it out. Would this equation also show that the wave is moving in the -x direction?

 

[Violagirl]

So I went back to look at this problem again and I think I found what the graph would look like for part a at time zero. I have the document attached. My question for B then, for the equation found for part B, which was:

y = A sin (kx + ∏/2)

does this mean then that the graph would still move in the -x direction but shift by half a wavelength to the left?