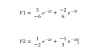SUMMARY
This discussion focuses on solving matrix differential equations to obtain the X matrix from given solutions V1 and V2. The user presents their solutions in exponential form and seeks clarification on how to derive the X matrix and verify the conditions x(0) = I (identity matrix) and dx/dt = AX. The correct formulation of the X matrix is established as X = (v1 v2), where v1 and v2 are defined as vectors. The user ultimately resolves an arithmetic error affecting their calculations.
PREREQUISITES
- Understanding of matrix differential equations
- Familiarity with exponential functions in differential equations
- Knowledge of matrix notation and operations
- Ability to differentiate matrices with respect to time
NEXT STEPS
- Learn how to compute the derivative of a matrix function
- Study the properties of matrix exponentials
- Explore the verification of initial conditions in matrix differential equations
- Investigate the application of the identity matrix in differential equations
USEFUL FOR
Students and professionals in mathematics, engineering, or physics who are working on matrix differential equations and need to understand the derivation and verification of solutions.