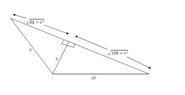
anemone said:
Find the maximum of $P(x)=\dfrac{x(\sqrt{100-x^2}+\sqrt{81-x^2})}{2}$.
$P(x)=\dfrac{x(\sqrt{100-x^2}+\sqrt{81-x^2})}{2} \\ \Rightarrow P'(x)=\dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2}+\dfrac{x}{2} \left ( \frac{-x}{ \sqrt{100-x^2}}+\frac{-x}{ \sqrt{81-x^2}} \right )=\dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2}-\dfrac{x^2}{2} \left ( \frac{1}{ \sqrt{100-x^2}}+\frac{1}{ \sqrt{81-x^2}} \right )=\dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2}-\dfrac{x^2}{2} \left ( \frac{\sqrt{81-x^2}+\sqrt{100-x^2}}{ \sqrt{100-x^2} \sqrt{81-x^2}} \right )= \left ( \dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2} \right ) \left ( 1-\dfrac{x^2}{\sqrt{100-x^2} \sqrt{81-x^2}} \right )$
$P'(x)=0 \Rightarrow \dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2}=0 \text{ or } 1-\dfrac{x^2}{\sqrt{100-x^2} \sqrt{81-x^2}}=0 \Rightarrow $
- $\dfrac{\sqrt{100-x^2}+\sqrt{81-x^2}}{2}=0 \Rightarrow \sqrt{100-x^2}+\sqrt{81-x^2}=0 \Rightarrow \sqrt{100-x^2}=-\sqrt{81-x^2}$
That cannot be true.
- $1-\dfrac{x^2}{\sqrt{100-x^2} \sqrt{81-x^2}}=0 \Rightarrow \dfrac{x^2}{\sqrt{100-x^2} \sqrt{81-x^2}}=1 \Rightarrow \sqrt{100-x^2} \sqrt{81-x^2}=x^2 \Rightarrow (100-x^2) (81-x^2)=x^4 \Rightarrow 8100-100x^2-81x^2+x^4=x^4 \Rightarrow 181x^2=8100 \Rightarrow x^2=\frac{8100}{181} \Rightarrow x= \pm \frac{90}{\sqrt{181}}$
$100-x^2 \geq 0 \Rightarrow x^2 \leq 100 \Rightarrow -10 \leq x \leq 10$
$81-x^2 \geq 0 \Rightarrow x^2 \leq 81 \Rightarrow -9 \leq x \leq 9$
The domain of $P(x)$ is $[-9,9]$.
$$\left ( -9, -\frac{90}{\sqrt{181}} \right ):P'(x)<0$$
$$\left [-\frac{90}{\sqrt{181}}, \frac{90}{\sqrt{181}} \right ]: P'(x)>0$$
$$\left ( \frac{90}{\sqrt{181}}, 9 \right ):P'(x)<0$$
So, $P(x)$ is decreasing at $\left ( -9, -\frac{90}{\sqrt{181}} \right )$, increasing at $\left [-\frac{90}{\sqrt{181}}, \frac{90}{\sqrt{181}} \right ]$ and decreasing at $\left ( \frac{90}{\sqrt{181}}, 9 \right )$.
So $P(x)$ achieves its maximum at $x=\frac{90}{\sqrt{181}}$, which is equal to $P \left ( \frac{90}{\sqrt{181}} \right )=\dfrac{\frac{90}{\sqrt{181}}\left (\sqrt{100-\left ( \frac{90}{\sqrt{181}} \right )^2}+\sqrt{81-\left ( \frac{90}{\sqrt{181}} \right )^2} \right )}{2}=\frac{45}{\sqrt{181}} \left ( \sqrt{\frac{18100-8100}{181}}+\sqrt{\frac{81 \cdot 181-8100}{181}} \right )=\frac{45}{181} \left ( \sqrt{10000}+\sqrt{6561} \right )=\frac{45}{181} \left ( 100+81 \right )=\frac{45 \cdot 181}{181} =45$