Maximum Length for Coaxial Cable in a 100 ns Noise Transfer Scenario

[usn7564]

Homework Statement

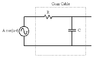
Signals from sources of different kinds are often very weak and very quick. To minimize the noise risk they're often led through coaxial cables. How long can one [coaxial cable] be if it has the capacitance 80pF / m and resistance 0.04 Ohm/m and you want to transfer noise that varies on 100 nano seconds?

Homework Equations

time constant = RC

The Attempt at a Solution

Right, so have the solution which basically just outlines what you do. You find the length L so that t is less or equal to RC. The cable is regarded as an RC circuit.

But I don't get the physics at all, what am I actually looking for? Noise that varies on 100 ns? (It's a direct translation but I honestly don't understand it better in my native tongue). What's special about t < RC in this scenario?

 

[skeptic2]

Is this problem from a textbook or did the professor create it? Either way it has serious flaws.

It seems that you are to calculate the length of cable that will behave as a low pass filter to reduce or eliminate noise that varies on 100 nS (whatever that means). The problem as stated doesn't give the beginning to noise ratio nor what signal to noise ratio is needed.

Furthermore, this is not how coax cables behave. In addition to capacitance and resistance, cables have inductance and when all three are combined in a coax, the impedance of the coax appears resistive. A coax cable does not behave as a low pass filter except that losses do tend to gradually increase with frequency. That means that whatever signal to noise ratio you start with is what you'll end up with.

 

[usn7564]

It's an exam question from an old exam. Course is basically forcing us to make simplified models of pretty much whatever asked, should probably have specified that. ie if you can't calculate it with the information given you make do with what you have.

Still don't understand it.

 

[gneill]

Presumably you're meant to model the coax as a simple RC filter.

The input signal has frequency components that have a period on the order of 100 ns. What angular frequency ω does that period correspond to? That frequency will specify your filter cut-off (corner) frequency...

 

[usn7564]

Solution doesn't even touch on the cutoff frequency or anything of the sort though. It does nothing except plays around with the time constant, I mean the actual mathematics involved is as elementary as it gets and. He puts the RC constant to 100ns.

Thanks for the help so far in any case.

 

[gneill]

I disagree with the given solution. The corner frequency of an RC low pass filter is
$$f_c = \frac{1}{2\pi \tau} = \frac{1}{2\pi R C}$$
Yes it involves the time constant $\tau$. But there should be a factor of $2\pi$ in there!

 

[usn7564]

Thanks again, have to refresh my memory on low pass filters (we only did a lab on it and the labs went to some more depth than what's covered in the course conventionally) but think I have the idea of what's going on at least.

 

[rude man]

I thnk the meaning is you want a 1st-order low-pass filter (R-C network) with cutoff radian frequency w = 1/(RC) where RC = 100 ns.

So, let x = length of line, then R = 0.04x and C = 80e-12x. Solve for x.